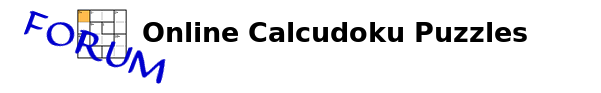Solución paso a paso de un 7x7 de sólo diferencias. Para este ejemplo usaré el crucigrama correspondiente al miércoles 10 de agosto de 2011, 7x7 difícil (9 puntos) (Identificación del crucigrama: 335050). Este calcudoku fue resuelto por únicamente 63 jugadores (menos del 20% de los jugadores activos en esa fecha). Sin embargo no requiere excesivo análisis.

Usaré parejas de números (en negro y tamaño pequeño en la parte inferior de las celdas) cuando se trate de los candidatos finales para esa caja, en tamaño grande (en el centro de la celda) para la solución final para esa celda, y usaré colores en general (y en un lateral de la caja para mostrar las diferentes opciones discutidas). Las “elipses” numeradas pequeñas hacen referencia a los distintos pasos a lo largo del procedimiento.
Podrían seguirse distintos caminos o métodos. Aquí aplicaremos el método de “prueba y error” durante el proceso de solución. Una buena estrategia inicial es determinar las celdas “aisladas” como la E2 y/o discutir las cajas “n-“ en las que n tiene un valor alto (menor número de combinaciones). Primeramente vemos que la caja “6-“ contiene la combinación 1-7 (única posibilidad, obviamente una caja “n-“ tiene p - n posibilidades, siendo p el tamaño del crucigrama, por ejemplo, “3-“ en un 9x9 tiene 9 - 3 = 6 posibilidades, es decir, 1-4, 2-5, 3-6, 4-7, 5-8 y 6-9; en nuestro caso 7 - 6 = 1, solamente una posibilidad, la obvia 1-7). Así pues escribimos 17 (1 ó 7) en las celdas F5 y F6.
Paso 1. En general es fácil determinar la paridad de celdas “aisladas” como la E2 que debe ser impar para completar la paridad par de las dos primeras filas (ver mi tópico “La paridad”; para mayor claridad, entrar en la versión en inglés de la página, en el “Calcudoku Forum”, donde Patrick Min acaba de añadir el gráfico que faltaba y que complementa el tema, no suministrado aún en la versión en español); en el puzzle que tratamos ahora es obvio que la paridad de la celda E2 es impar dado que 2-6 no es una combinación posible para la caja E2-E3, así las otras dos posibilidades, 1-5 y 3-7, sólo contienen números impares. Puesto que 3-7 no es posible (no se podría situar un 6 en la columna E porque generaría un segundo 3), la solución para la caja es 1-5, luego E2 = 1 y E3 = 5.

Paso 2 (mostrado en azul claro). 2-6 no es válida en C3-C4 porque el 7 de la fila 3 tendría que ir a A3, con un 6 en A4 y, consecuentemente, ningún 5 se podría situar en la fila 4. Así, 3-7 es la única posibilidad para esta caja “4-“ y escribimos 37 en las celdas C3-C4.
Paso 3 (mostrado en rojo). 1-5 no es válida en C6-C7 porque el 7 de la columna D tendría que ir a D5, con un 6 en C5, y ningún 5 podría situarse en la columna D (ahora la pareja 3-7 en C3-C4 inhibe el que cualquier 5 se posicione en D1 o D2). Entonces, puesto que 3-7 y 1-5 no son posibles, C6-C7 debe ser 2-6 y escribimos 26 en estas celdas.
Paso 4. Un 1 no es posible en C5 (requeriría un 2 en D5 pero ya existe un 2 en la columna D, en D3) luego C1= 1 y consecuentemente D1 = 3.
Paso 5 (mostrado en naranja). 7 no es válido en G1 porque produce un 5 en G2 y ningún 7 se podría situar en la fila 2. Así, el 7 de la fila 1 debe ser colocado (junto con un 6) en A1-B1 y escribimos 67 en estas dos celdas.
Esta es la situación actual:

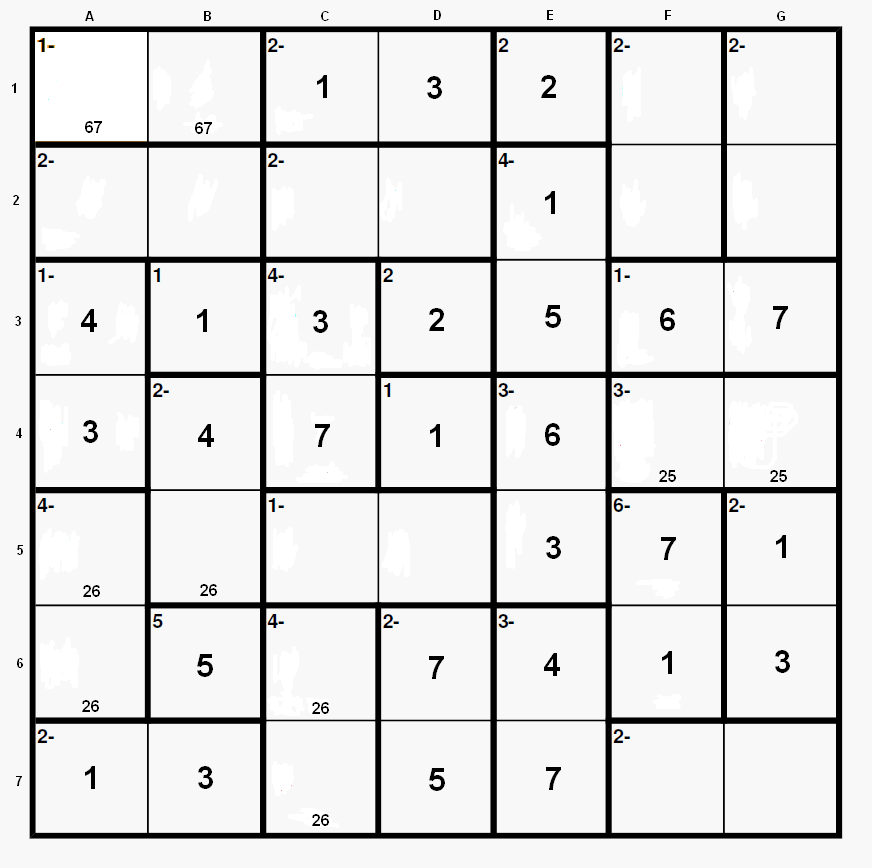
Ahora continuemos con el siguiente gráfico:

Paso 6 (mostrado con números en amarillo).
1) Resolvemos ahora la caja “4-“ en C3-C4. El 7 en C3 no es posible (con C4 = 3) dado que el 6 de la fila 3 tendría que estar necesariamente en A3 (no podría estar dentro de F3-G3 al estar sus números adyacentes, 5 y 7, presentes en la fila 3) y, puesto que 6-7 no sería ahora posible en A3-A4 (de otro modo entraría en conflicto con A1-B1), A4 = 5, la caja “3-“ en F4-G4 sería 4-7 con G4 = 7, F4 = 4, y el 4 de la fila 3 iría a G3 (F3 = 3) haciendo imposible situar cualquier 4 en la fila 1. Entonces C3 = 3 y C4 = 7.
2) Ahora el 4 de la fila 3 no puede estar dentro de la caja “1-“ de F3-G3 (los números adyacentes necesarios para el “1-“, 3 y 5, ya están presentes en la fila 3). Por lo que A3 = 4. También G3 = 7 y F3 = 6.
Paso 7 (mostrado en azul oscuro). Analizamos ahora la caja “3-“ en F4-G4. La combinación 3-6 no es posible porque requiere A4 = 5, E4-E5 sería 4-7 con E4 = 4 y E5 = 7. Obsérvese que ahora ningún 7 podría situarse en la fila 7 (los 5’s en A4 y B6 inhibirían el que un 7 estuviera en A7, B7 o D7, las demás celdas de la fila 7 “borradas” por 7’s en las columnas). Así, la caja “3-“ en F4-G4 debe ser 2-5 y escribimos 25 en esas celdas. Y, como consecuencia, A4 = 3 (para completar la caja A3-A4).
Paso 8 (mostrado en violeta). La combinación 1-5 no es posible para la caja “4-“ en A5-A6. Obsérvese que un 5 no puede ir a F2 o G2 (dado que debe existir un 5 en F1 o G1 y F4-G4 contienen otro 5 por lo que se “borran” simultáneamente de nuevos 5’s las columnas F y G); un 5 no es posible en D2 (3 y 7 en C3-C4), así que el 5 de la fila 2 iría a C2 con un 7 en D2 y entonces ningún 5 podría situarse en la columna D (un 5, por ejemplo, en D7 requeriría un 3 ó un 7 en D6, ambos ya presentes en la columna D). Luego A5-A6 es 2-6 y escribimos 26 en esas celdas.
Adicionalmente A7 = 1, B7 = 3. El 7 de la fila 7 va a E7 (E6 = 4).
Paso 9 (los números, aunque mostrados en verde esta vez, son números definitivos). Ahora completamos la caja “3-“ en E4-E5. E5 = 3, E4 = 6. Y también B4 = 4 con B5 pudiendo tomar los valores 2 ó 6 (así escribimos 26 en la celda B5).
El 5 de la fila 7 debe ir al único asiento libre de D7 (no dentro de “2-“ en F7-G7 debido a que los números adyacentes, 3 y 7, ya están presentes en la fila 7). Ahora D6 = 7 (3 in D1). Por tanto F6 = 1 y F5 = 7. El 1 de la fila 5 va a G5 (1’s ya en las columnas C y D) y G6 = 3.
Esta es la situación después del paso 9:
Terminamos el crucigrama con dos simples pasos (siguiente gráfico):
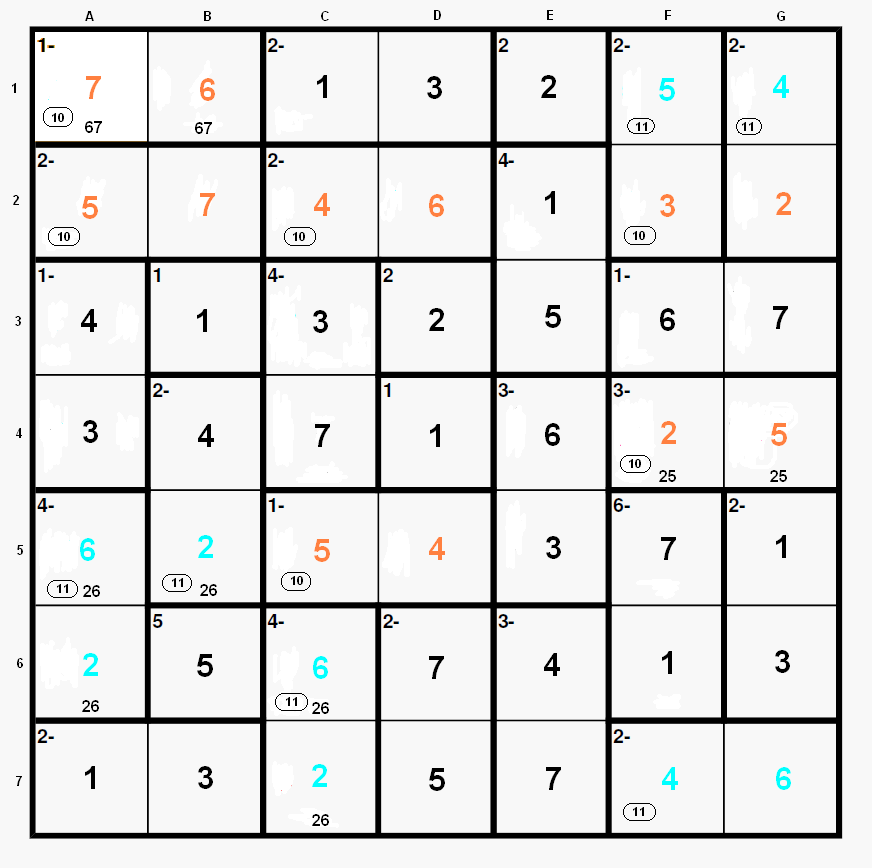
Paso 10 (mostrado en naranja).
A1 = 7 (2-6 en A5-A6), B1 = 6.
A2 = 5, B2 = 7 (3 en B7).
Fila 5: C5 = 5, D5 = 4.
Fila 2: C2 = 4, D2 = 6, F2 = 3 (3 en G6), G2 = 2.
Fila 4: F4 = 2, G4 = 5.
Paso 11 (mostrado en azul claro).
El 6 en B1 fuerza B5 = 2, A5 = 6, A6 = 2, C6 = 6, C7 = 2.
G7 = 6 (6 en F3), F7 = 4, G1 = 4 y F1 = 5.
Y esta es la solución “oficial”: