The solution of a 6x6 and a 9x9 puzzles with "strange cages"
| Author |
Message |
clm 
Posted on: Sat Nov 12, 2011 12:00 am
Posts: 857
Joined: Fri May 13, 2011 6:51 pm

|
 The solution of a 6x6 and a 9x9 puzzles with "strange cages" Hi, Patrick: Could you please test with your solver these two puzzles?. The idea is to verify the number of solutions (if more than one). I assume your solver provides that info. I am supposing that the probability for the unique solution increases with the size of the puzzle, in other words, if we design a puzzle 9x9, with some restrictions (conditions) here and there, the number of solutions decreases with respect to a similar construction with a lower size puzzle like, i.e., a 6x6 (we are talking about a designer who has not a software able to make the necessary modifications to the puzzle to insure the final unicity of the solution). I have designed these two puzzles, a 6x6 and a 9x9, using those “strange cages” referred to in the topic “The shape of the cages (structure and names)”. A very reduced number of those cages (4 in the 6x6, 9 in the 9x9) occupy the full puzzle. Those cages have a “hole” inside (what I called a 2D “Keops hole”). It would also be interesting to know the time spent by the computer to find the first solution for each puzzle as well as your “solver rating” for both. Thanks, clm.  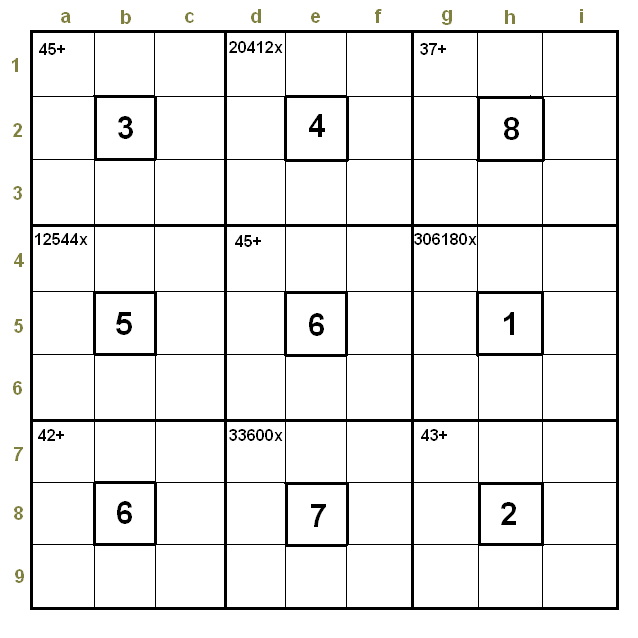
|
|

|
 |
giulio 
Posted on: Mon Nov 14, 2011 8:02 am
Posts: 54
Joined: Thu Nov 03, 2011 8:52 am

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca Hi clm,
2700x has the prime factors: 2233355; 3600 has the prime factors: 22223355
Unless I have made mistakes, only the following combinations are possible:
2700x - 66553111 / 65533211 / 55433311 / 55333221 => always at least once 1, once 3, twice 5
3600x - 66554111 / 65543211 / 55443311 / 55433221 => always at least once 1, once 4, twice 5
If you choose for 2700x the solution 66553111, the cage 28+ only admits a single combination: 64443322, bacause it can only have no 5, no 1, once 6, and twice 3 (I only write the limitations. The maximum count for what I don't mention is 3).
But that is not compatible with any of the possible 3600x combinations, because, to avoid conflicts with 18+, it cannot have any 4.
If you choose for 3600x the solution 66554111, the cage 28+ doesn't admit any combination at all.
If you choose for 2700x the solution 65533211, the cage 28+ can only have no 5, once 3, once 1, twice 2, and twice 6. This makes possible for 28+ only the combination 66443221.
This means that 3600x can have once 6, once 4, twice 3, once 2, and twice 1.
Of the remaining three combinations of 3600x (65543211 / 55443311 / 55433221), the second is not possible because it has two 4s; the third is not possible because it has two 2s; only 65543211 is possible.
When considering the the combined limitations imposed by 2700x and 3600x, cage 31+ can have twice 6, once 5, twice 4, once 3, twice 2, and once 1.
This means that 31+ admits the combination 66544321. It remains to be seen whether or how many permutations are possible.
OK. We still have to look at the following combinations
2700x - 55433311 / 55333221 => always at least once 1, twice 3, twice 5
3600x - 55443311 / 55433221 => always at least once 1, twice 3, once 4, twice 5
With 2700x set to 55433311, 28+ can have no 5, no 3, twice 4, and once 1. No combinations for 28+ are possible.
With 3600x set to 55443311, 28+ can have no 5, once 4, once 3, once 1. The only possible combination for 28+ is 66632221, but that is incompatible with the remaining combination for 2700x (55333221) because it requires a 3 in each column.
We are left with 5533221 for 2700x and 55433221 for 3600x.
If we start from 2700x, we see that 28+ can have no 5, no 3, twice 2, and twice 1. This gives us two combinations for 28+: 66642211 and 66444211. But they are both incompatible with the only combination left for 3600x (55433221), because it requires twice a 2 and once a 4.
All in all, we are left with the following combinations:
2700x 65533211; 28+ 66443221; 3600x 65543211; 31+ 66544321.
To check whether there are possible solutions and how many, you definitely need a program, though, because by placing the 5s alone you already generate 32 possible permutations.
|
|

|
 |
clm 
Posted on: Mon Nov 14, 2011 10:43 am
Posts: 857
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca giulio wrote: Hi clm,
2700x has the prime factors: 2233355; 3600 has the prime factors: 22223355
Unless I have made mistakes, only the following combinations are possible:
2700x - 66553111 / 65533211 / 55433311 / 55333221 => always at least once 1, once 3, twice 5
3600x - 66554111 / 65543211 / 55443311 / 55433221 => always at least once 1, once 4, twice 5
... Hi, giulio: I thought nobody was going to try it, you really made a big effort. I have to study your analysis in depth, very interesting line of thinking, and when I have a conclusion I will give you some comment (before submitting the solutions to the Forum I am waiting to see if the Patrick's solver can confirm the number of solutions, you are right about the necessity of a program for that, but even for this 6x6 you are initially referring to, if the solution I have were unique, the solver rating could be > 300 perhaps, in the case of the 9x9 who knows...). However, an initial comment, is there any reason why you have initially excluded in your analysis the combination 66552211 for the 3600x? (in the case of the 65532221 it is obvious, three 2's, and there is already a 2 in b2). Apart of this, I can provide an initial premise. Considering the addition, 63, of three columns or three rows, it can be quickly seen that "2700x" (+) = 26 so the only combination is 65533211 having the other three combinations values of 24, 25 and 28. Now, the "28+" is made by the rest of the numbers in columns d, e and f, that is, 66443221. Similarly, "3600x" (+) = 27 and the only combination is 65543211, having the other four combinations sums of 25, 26, 28 and 29. Consequently, "31+" = [6, 6, 5, 4, 4, 3, 2, 1]. The real problem is not determining the numbers that compose those "strange cages" (with that terrible "black hole" in the center consuming our minds) but distributing them along the puzzle.
|
|

|
 |
pnm 
Posted on: Mon Nov 14, 2011 2:50 pm
Posts: 3305
Joined: Thu May 12, 2011 11:58 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca Hi clm, clm wrote: Could you please test with your solver these two puzzles?
Would it be possible for you to send me the puzzles in this format: 6 31,+,a1b1c1a2c2a3b3c3 etc. ? The first line has the dimension of the puzzle. (any other simple file format you can suggest is welcome) (the current file format that my solver uses is too cumbersome and outdated, I'll probably end up having to write a converter between a simple format and the "internal" format..) thanks, Patrick
|
|

|
 |
clm 
Posted on: Mon Nov 14, 2011 3:25 pm
Posts: 857
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca pnm wrote: Hi clm, clm wrote: Could you please test with your solver these two puzzles?
Would it be possible for you to send me the puzzles in this format: 6 31,+,a1b1c1a2c2a3b3c3 etc. ? The first line has the dimension of the puzzle. (any other simple file format you can suggest is welcome) (the current file format that my solver uses is too cumbersome and outdated, I'll probably end up having to write a converter between a simple format and the "internal" format..) thanks, Patrick Thanks, Patrick. If I have understood you correctly, for the 6x6, it would be: 6 31,+,a1b1c1a2c2a3b3c3 2,b2 2700,x,d1e1f1d2f2d3e3f3 4,e2 3600,x,a4b4c4a5c5a6b6c6 3,b5 28,+,d4e4f4d5f5d6e6f6 5,e5 For the 9x9, it would be: 9 45,+,a1b1c1a2c2a3b3c3 3,b2 20412,x,d1e1f1d2f2d3e3f3 4,e2 37,+,g1h1i1g2i2g3h3i3 8,h2 12544,x,a4b4c4a5c5a6b6c6 5,b5 45,+,d4e4f4d5f5d6e6f6 6,e5 306180,x,g4h4i4g5i5g6h6i6 1,h5 42,+,a7b7c7a8c8a9b9c9 6,b8 33600,x,d7e7f7d8f8d9e9f9 7,e8 43,+,g7h7i7g8i8g9h9i9 2,h8 Best.
|
|

|
 |
pnm 
Posted on: Mon Nov 14, 2011 4:01 pm
Posts: 3305
Joined: Thu May 12, 2011 11:58 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca clm wrote: Thanks, Patrick. If I have understood you correctly, for the 6x6, it would be:
6
31,+,a1b1c1a2c2a3b3c3
2,b2
2700,x,d1e1f1d2f2d3e3f3
4,e2
3600,x,a4b4c4a5c5a6b6c6
3,b5
28,+,d4e4f4d5f5d6e6f6
5,e5
Yes, thanks. I let the solver run for one minute on the 6x6, after which it had found 255 valid solutions. Do you want me to let it run for longer? Patrick
|
|

|
 |
clm 
Posted on: Mon Nov 14, 2011 4:27 pm
Posts: 857
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca pnm wrote: clm wrote: Thanks, Patrick. If I have understood you correctly, for the 6x6, it would be:
6
31,+,a1b1c1a2c2a3b3c3
2,b2
2700,x,d1e1f1d2f2d3e3f3
4,e2
3600,x,a4b4c4a5c5a6b6c6
3,b5
28,+,d4e4f4d5f5d6e6f6
5,e5
Yes, thanks. I let the solver run for one minute on the 6x6, after which it had found 255 valid solutions. Do you want me to let it run for longer? Patrick Thank you, I do not think it is necessary to continue, but I am surprised for the high number of solutions (how many? symmetries or totally different?...). Would it be possible for you to show only two of them?. And the solver rating for the 6x6?. And what about the 9x9?. With respect to the file format, the last used is Ok, anyway I may suggest, according to the "international terminology" I am "presenting in society", for instance, for the 6x6: "31+" (a1-b1-c1-a2-c2-a3-b3-c3); b2 = 2; "2700x" (d1-e1-f1-d2-f2-d3-e3-f3); e2 = 4; "3600x" (a4-b4-c4-a5-c5-a6-b6-c6); b5 = 3; "28+" (d4-e4-f4-d5-f5-d6-e6-f6); e5 = 5; Is this more friendly? This conversation has brought to my attention that I have to include the size of the puzzle at the very beginning, for instance: C = 6 (C for Calcudoku).
|
|

|
 |
pnm 
Posted on: Mon Nov 14, 2011 4:31 pm
Posts: 3305
Joined: Thu May 12, 2011 11:58 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca clm wrote: Thank you, I do not think it is necessary to continue, but I am surprised for the high number of solutions (how many? symmetries or totally different?...). Would it be possible for you to show only two of them?. And the solver rating for the 6x6?.
Sure, I'll post a few solutions. The rating depends on how many configurations the solver has to try, so for that I'd have to let it run to a finish.. clm wrote: And what about the 9x9?. Still running. clm wrote: With respect to the file format, the last used is Ok, anyway I may suggest, according to the "international terminology" I am "presenting in society", for instance, for the 6x6:
"31+" (a1-b1-c1-a2-c2-a3-b3-c3);
b2 = 2;
That format would not be consistent, because the single cell cages are specified differently. Of course it's possible to change the converter to accept those cases, but I'd prefer a more consistent format. In this case the 2nd line would become: "2+" (b2); for example. Patrick
|
|

|
 |
jomapil 
Posted on: Mon Nov 14, 2011 4:43 pm
Posts: 246
Location: Lisbon, Portugal
Joined: Sun Sep 18, 2011 5:40 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca In my modest opinion, Clm, Patrick is right: It's more consistent and uniform.
_________________Visit http://www.calcudoku.org the most interesting and addictive site of puzzles.
|
|

|
 |
pnm 
Posted on: Mon Nov 14, 2011 4:53 pm
Posts: 3305
Joined: Thu May 12, 2011 11:58 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca In addtion, I like to reduce typing as much as possible
Note that in my suggested format:
6
31,+,a1b1c1a2c2a3b3c3
I could reduce it still by one character by defining:
6
+31,a1b1c1a2c2a3b3c3
(Also note that for the single cage you wrote:
2,b2
and as a result, I had to add a special case to the converter such that
it detects an operator is missing..)
And note the typing overhead for your specification:
"31+" (a1-b1-c1-a2-c2-a3-b3-c3);
- quotes
- parentheses
- dashes
- a space
- a semicolon at the end...
Granted, the dashes make the cell list a bit more readable.
Patrick
|
|

|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
|

|