
Full tables: 5x5 puzzles with negative numbers
Full tables: 5x5 puzzles with negative numbers. Actually, in this site, there are not puzzles of the type, for instance, -3 to +3 (7x7 puzzle), so in this topic we will limit the comments to the 5x5 puzzles with negative numbers (-2 to +2). The idea is to help a little (comments and observed mistakes welcome) in the quick determination of the possible combinations for the 2-cell and 3-cell cages (4-cell cages are not included here though the philosophy would be the same).
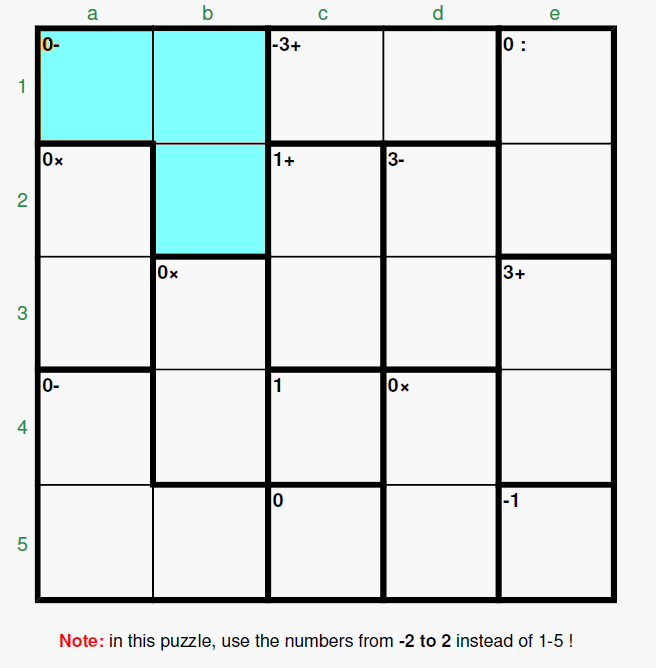
(this was the Puzzle id: 403420 appeared on Monday Jan 30, 2012)
Some initial comments:
In the puzzles with positive numbers, when we have a subtraction cage, we always start with the higher number and then subtract the others until we arrive to the result shown in the cage (later we may permute, inside the cage, the position of the candidates, considering the rest of the restrictions). For instance, a 3-cell L-shape cage “3-“ in a 9x9 puzzle has the possible combinations [1, 1, 5], [2, 2, 7], [3, 3, 9] (these with the repeated number in the corners) or [1, 2, 6], [1, 3, 7], [1, 4, 8], [1, 5, 9], [2, 3, 8] and [2, 4, 9] (these combinations may rotate the candidates). The result (3 in this case) is always lower than the size of the puzzle.
The main difference now, with the negative numbers, for the subtraction cages, is that we may start in “any” number inside the cage, being the result negative or positive (and the value of “r” in an “r-“ cage may be equal or higher than the size of the puzzle, as we see in the tables, when 3 cells are in-line or 3 cells are in L-shape). Mathematically, if we have an expression like this:
diff = a - b - c - d then |diff| <= |a| + |b| + |c| + |d|
(the absolute value of the difference is minor or equal to the sum of the absolute values of the numbers involved, being those numbers themselves positive or negative),
so it may happen, for instance for a 3-cell L-shape cage with the combination [-2, 2, 2], that the result is the cage “-6-“. The important thing with the subtractions is to be careful with the signs since two consecutive “-“ produce a “+”.
For the multiplication (and exactly the same for the division) it is necessary to remind the rule of the signs, which is also “iterative”:
(+) x (+) = (+)
(+) x (-) = (-)
(-) x (+) = (-)
(-) x (-) = (+) but, for the result of the cage, we may operate first with the absolute values of the operands and later consider the signs because if
prod = a x b x c then |prod| = |a| x |b| x |c|
i.e. a 2-cell cage “-4x” would only admit [-2, 2] with the same rules applying to the division, for instance, a 3-cell L-shape cage “-1:” = [-2, -2, -1], [-2, 1, 2], [-1, 1, 1], [-1, 2, 2]. It would not be very significant to give all combinations for the multiplication and the division cages so we will include only the addition and subtraction cages in this topic. A zero “has not sign” (we may assign to it a + or a -), the result in a multiplication cage is always zero, so “0x” or, in the case of the division (“0:”) only one zero could be inside the cage and that zero is assumed to be the dividend (the division by zero is not allowed).
Observe a curious thing in the subtraction tables: “the symmetry” with respect to an horizontal axis, changing the sign of the result (keeping the operator) is equivalent to changing the sign of all the operands for all the involved combinations.



![Smile [smile]](./images/smilies/msp_smile.gif) ) if necessary; that notation is very comfortable if you write the combinations apart (pen and paper) because you may suppress the parenthesis but it is not very comfortable with the PC keyboards (special characters).
) if necessary; that notation is very comfortable if you write the combinations apart (pen and paper) because you may suppress the parenthesis but it is not very comfortable with the PC keyboards (special characters).