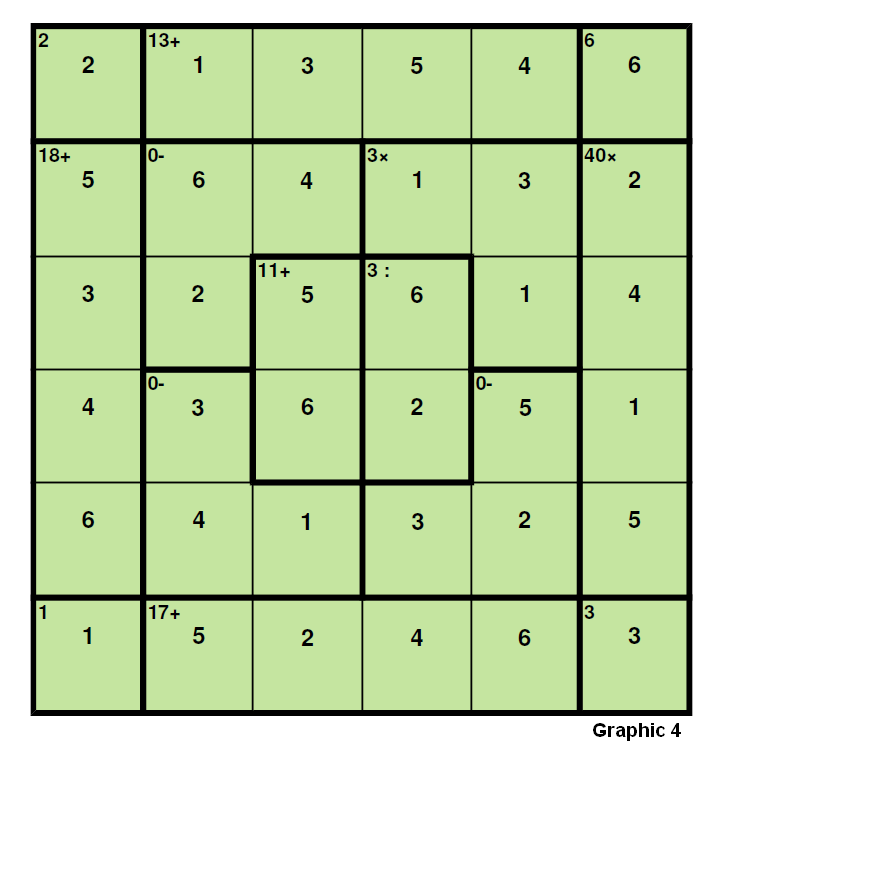
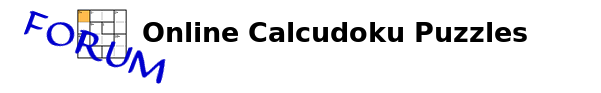Previous determination of cages in a 6x6 difficult
Previous determination of cages in a 6x6 difficult. (Oriented to beginners / medium players)
This is the 6x6 “difficult” (solver rating 44.3) (saturday May 19, 2012). Though many puzzlers have solved it, the idea of opening this post is to show a different point of view on the analysis that can decrease the time for the solution and can avoid many “trial and error” (TAE).
The main idea is determining the “0-” cages arithmetically. We will solve this puzzle in three steps:
First: We define which will be the cages (the only possible combinations) (graphic 1).
Second: We assign the combinations found to the proper positions in the grid (Graphic 2).
Third: We easily complete the rest of the puzzle (Graphic 3).
In order to better understand the first step we must remind that, in a 6x6,
always, the numbers in the inner area (the 4x4 inner box) are the corners plus twice the numbers 1 thru 6; it’s an easy demonstration, very intuitive, which is anyway explained in the post “Why in a 4x4 numbers in corners are those in inner area (2)” in the section “Solving strategies and tips”. (Comment: This rule is valid for puzzles of any size, i.e., in a 7x7, the 25 numbers in the inner area would be the corners plus thrice the numbers 1 thru 7, ... ).
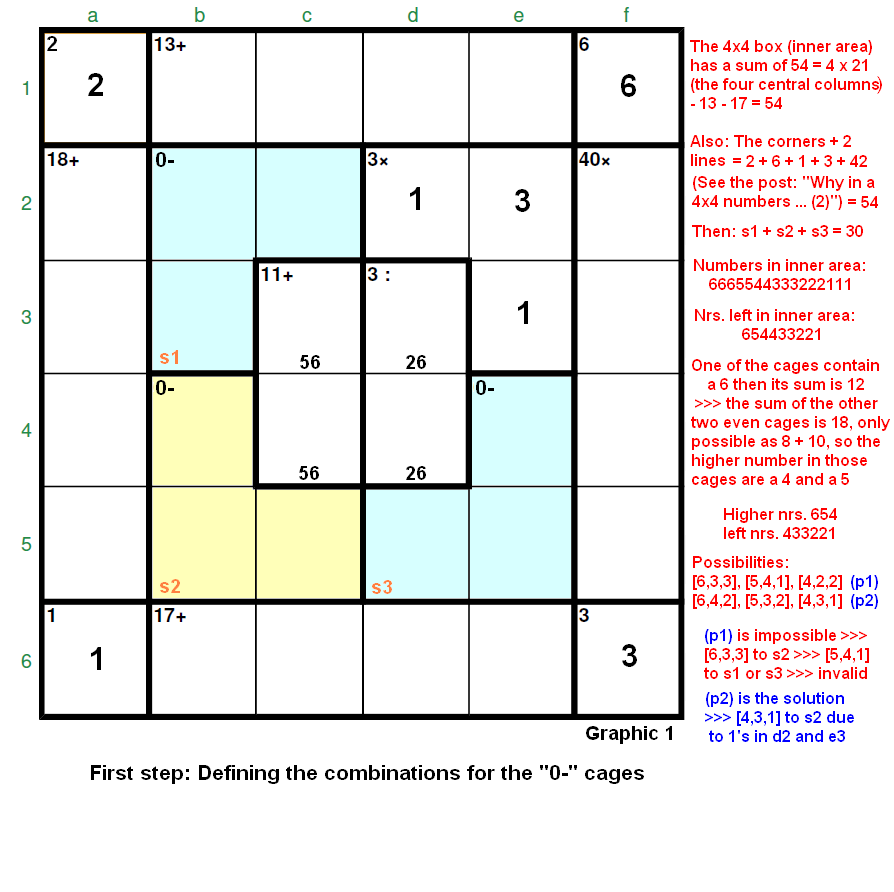
Graphic 2: If we assign [6,4,2] to s3 >>> b6 = 6. Now, since the columns b and c must sum 42, being s1 = [5,3,2] (and consequently c2 = 2), we are left with a sum of 7 for the three cells in gray colour and that’s impossible, what means that [5,3,2] must go to s3 and [6,4,2] to s1.
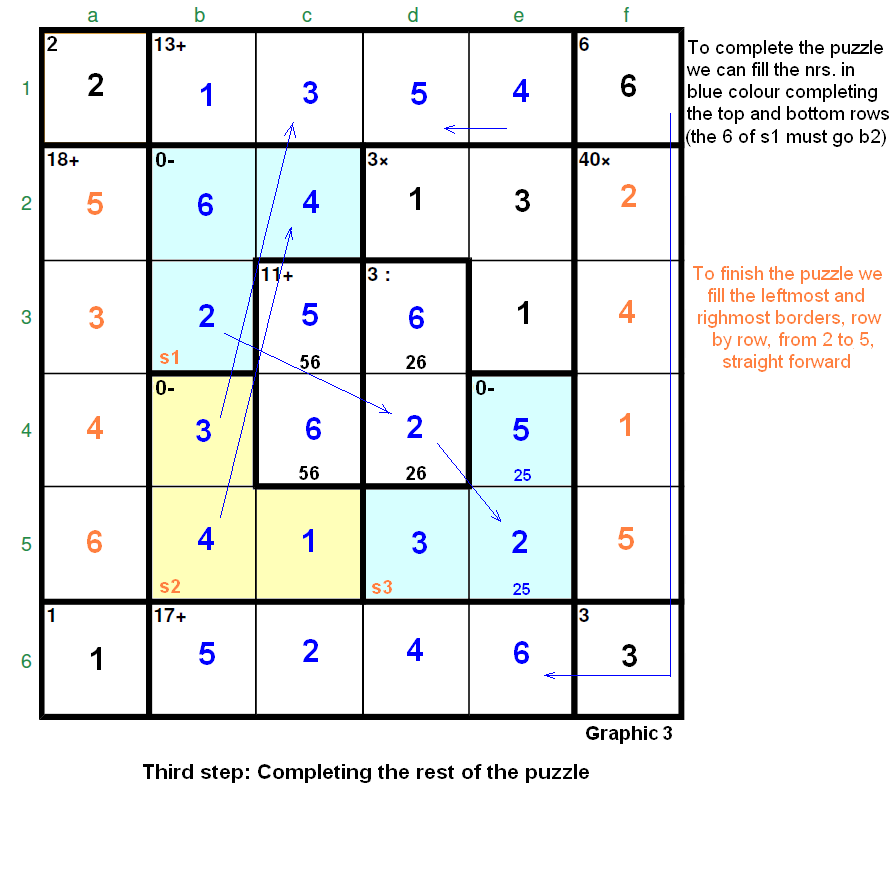
Graphic 3: We complete the puzzle. We start (since [5,3,2] goes to s3) with d5 = 3 >>> e4-e5 = [2,5] then e6 = 6, e1 = 4 >>> d6 = 4, d1 = 5. Additionally d5 = 3 >>> b4 = 3 >>> c1 = 3 >>> b1 = 1 >>> c5 = 1 >>> b5 = 4 >>> c2 = 4. The rest of numbers in blue colour are very easy to follow. And finally we place the numbers in brown colour.
The “official solution”: