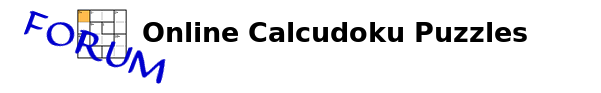[quote="clm"]
Step by step solution of a 7x7 subtractions only. (This is a retransmission of the topic with larger graphics and enhanced resolution).
For this example I will use the wednesday Aug 10, 2011, 7x7 difficult puzzle (9 points) (Puzzle id: 335050). This puzzle was solved by only 63 players (less than a 20% of the active players in that moment). However it does not require excessive analysis.
I will use pairs of numbers (in black and small size in the lower part of the cell) when those are the final candidates for that cage, in big size (in the center of the cell) for the final solution for that cell, and I will use colors in general (and in one side of the cages to show the different options discussed). The small numbered “ellipses” refer to the steps along the procedure.
Different ways or methods may be followed. The method of “test and error” will be applied during the process of solution. A good inicial strategy is determining the “isolated” cells like E2 and/or discussing the cages “n-“ where n has a high value (less number of combinations). First we see that the cage “6-“ contains the combination 1-7 (only one possibility, obviously a cage “n-“ has p - n possibilities, being p the size of the puzzle, i.e., “3-“ in a 9x9 has 9 - 3 = 6 possibilities, that is, 1-4, 2-5, 3-6, 4-7, 5-8 and 6-9; in our case 7 - 6 = 1, only one possibility the obvious 1-7). So we write 17 (1 or 7) in cells F5 and F6.
Step 1. In general it is easy to determine the parity of “isolated” cells like E2 that must be odd to complete the even parity of the first two rows (see my topic “The parity”); in this particular puzzle it is obvious anyway that the parity of the cell is odd since 2-6 is not a possible combination for the cage E2-E3, so the other two possibilities, 1-5 and 3-7, are made with odd numbers. Since 3-7 is not possible (a 6 could not be located in column E because another 3 would appear), the solution for the cage is 1-5, so E2 = 1 and E3 = 5.

Step 2 (shown in light blue). 2-6 is not valid in C3-C4 because the 7 of row 3 should go to A3, with a 6 in A4, and consequently no 5 could be located in row 4. So the 3-7 is the only possibility for this cage “4-“ and we write 37 in cells C3-C4.
Step 3 (shown in red). 1-5 is not valid in C6-C7 because the 7 of column D should only go to D5, with a 6 in C5, and no 5 could be located in column D (now the 3-7 in C3-C4 inhibit any 5 to be in D1 or D2). Then, since 3-7 and 1-5 are not possible, C6-C7 must be 2-6 and we write 26 in these cells.
Step 4. A 1 is not possible in C5 (it would require a 2 in D5 but there is a 2 already in column D, in D3) so C1= 1 and consequently D1 = 3.
Step 5 (shown in orange). 7 is not valid in G1 because it produces a 5 in G2 and no 7 could be located in row 2. So the 7 of row 1 must be placed (with a 6) in A1-B1 and we write 67 in these two cells.
This is the actual situation:

Now let’s continue with the following graphic:

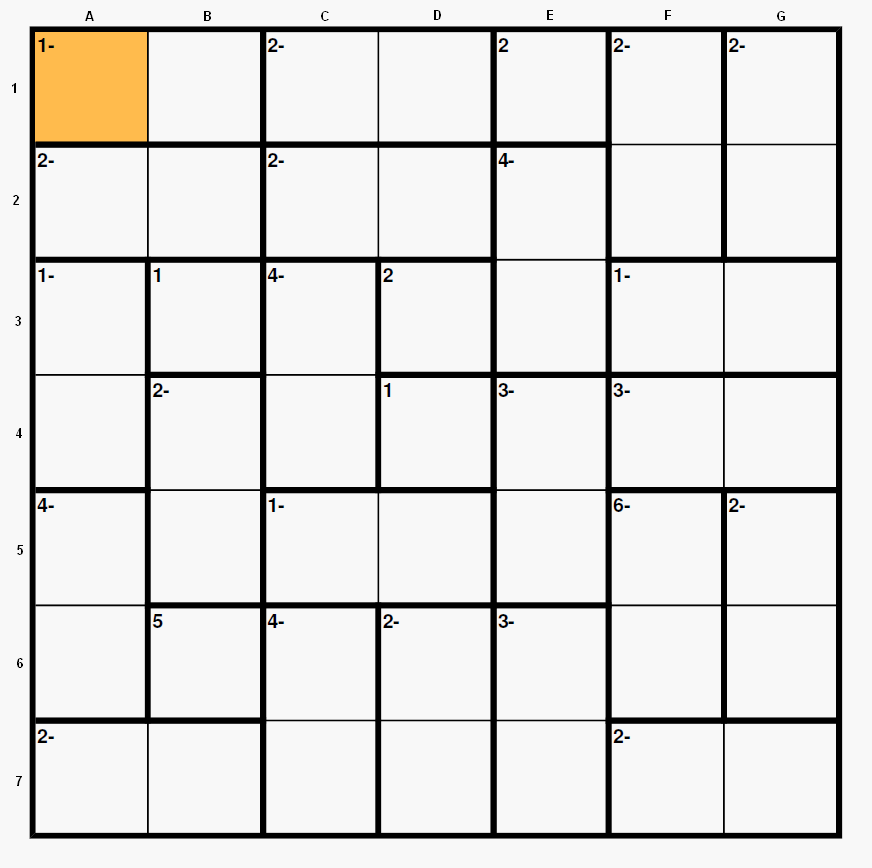
Step 6 (shown with numbers in yellow).
1) We solve now the cage “4-“ in C3-C4. A 7 in C3 is not possible (with C4 = 3) since the 6 of row 3 should necessarily be in A3 (could not be inside F3-G3 because of the contiguous numbers, 5 and 7, already present in row 3), and since 6-7 would not be possible now in A3-A4 (otherwise there is a conflict with A1-B1), A4 = 5, the cage “3-“ in F4-G4 would be 4-7 so G4 = 7, F4 = 4, and the 4 of row 3 would go to G3 (F3 = 3) making impossible to have any 4 in row 1. Then C3 = 3 and C4 = 7.
2) Now the 4 of row 3 is not inside the cage “1-“ of F3-G3 (the contiguous numbers necessary for “1-“, 3 or 5, are already present in row 3). So A3 = 4. Also G3 = 7 and F3 = 6.
Step 7 (shown in dark blue). We analyze now the cage “3-“ in F4-G4. The combination 3-6 is not possible because it requires A4 = 5, E4-E5 would be 4-7 with E4 = 4 and E5 = 7. Observe that now no 7 could be placed in row 7 (the 5’s in A4 and B6 would inhibit the 7 to be in A7, B7 or D7, the other cells or row 7 “erased” by 7’s). So the cage “3-“ in F4-G4 must be 2-5 and we write 25 in those cells. And as a consequence A4 = 3 (to complete the cage A3-A4).
Step 8 (shown in violet). The combination 1-5 is not possible for the cage “4-“ in A5-A6. Observe that a 5 can not be located in F2 or G2 (since it must be a 5 in F1 or G1 and F4-G4 contain a 5 so “erasing” columns F and G simultaneously); a 5 is not possible in D2 (3 and 7 in C3-C4), so the 5 of row 2 would go to C2 with a 7 in D2 and then no 5 could be positioned in column D (a 5, i.e., in D7 would require a 3 or a 7 in D6 both already present in column D). So A5-A6 is 2-6 and we write 26 in those cells.
Additionally A7 =1, B7 = 3. The 7 of row 7 goes to E7 (E6 =4).
Step 9 (numbers, although shown in green this time, are final numbers). We now complete the cage “3-“ in E4-E5. E5 = 3, E4 = 6. And also B4 = 4 with B5 being 2 or 6 (we write 26 in cell B5).
The 5 of row 7 must go to the only free seat D7 (not inside “2-“ in F7-G7 due to the contiguous numbers 3 and 7 already present in row 7). Now D6 = 7 (3 in D1). Then F6 = 1 and F5 = 7. The 1 of row 5 goes to G5 (1’s already in columns C and D) and G6 = 3.
This is the situation after step 9:
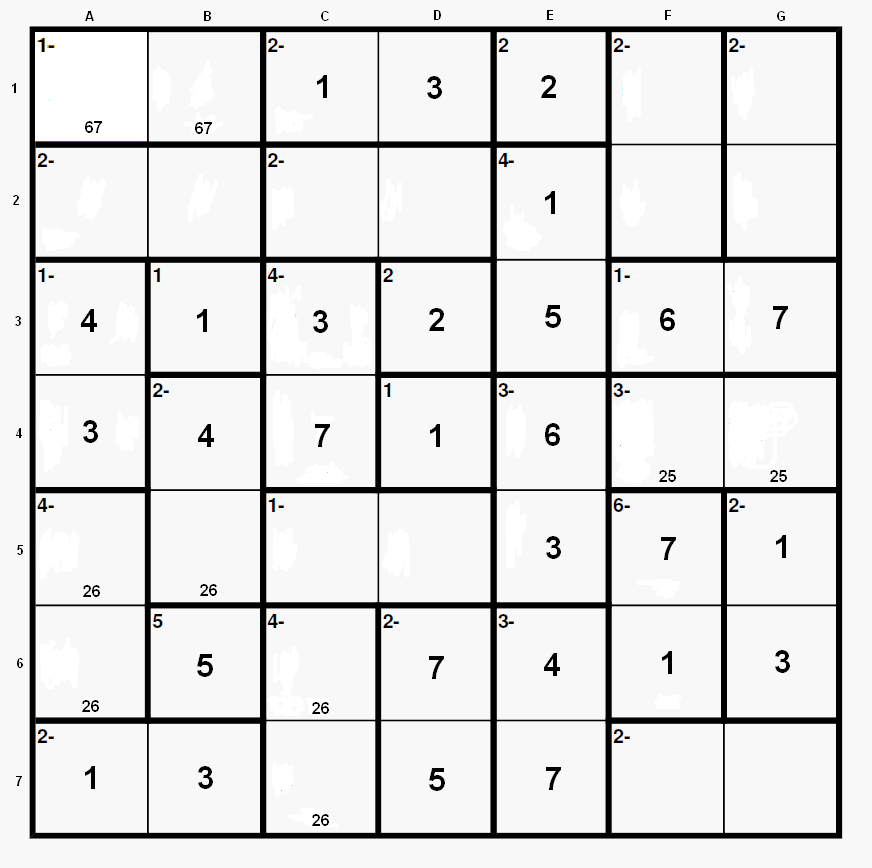
Now let’s finish the puzzle with two simple steps (next graphic):
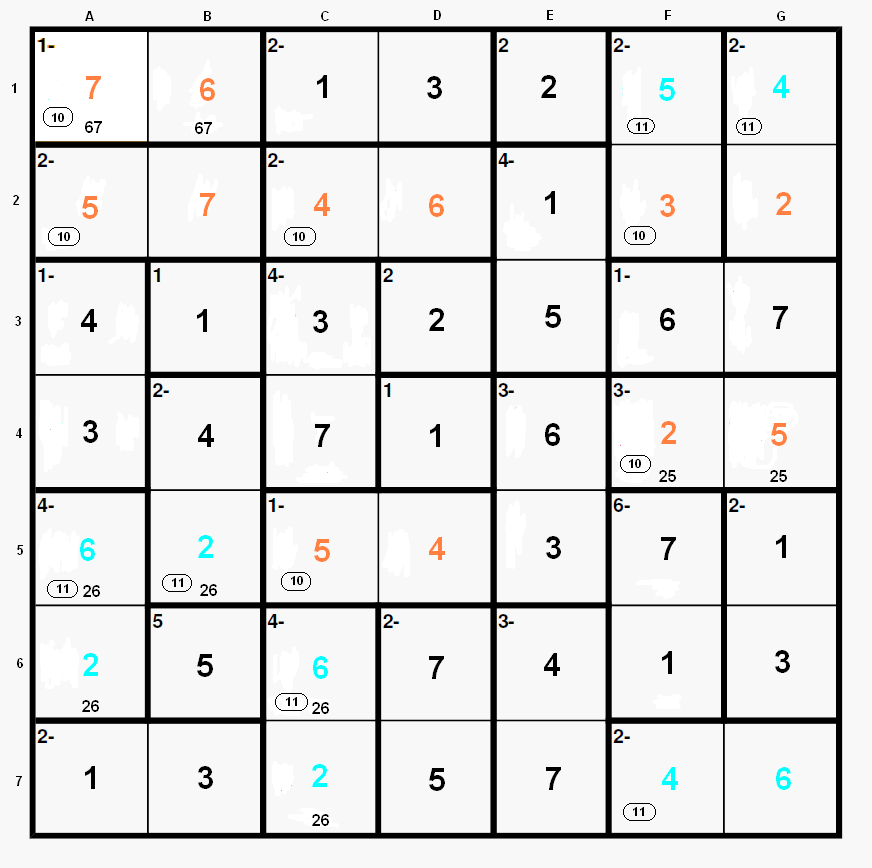
Step 10 (shown in orange).
A1 = 7 (2-6 in A5-A6), B1 = 6.
A2 = 5, B2 = 7 (3 in B7).
Row 5: C5 = 5, D5 = 4.
Row 2: C2 = 4, D2 = 6, F2 = 3 (3 in G6), G2 = 2.
Row 4: F4 = 2, G4 = 5.
Step 11 (shown in light blue).
The 6 in B1 forces B5 = 2, A5 = 6, A6 = 2, C6 = 6, C7 = 2.
G7 = 6 (6 in F3), F7 = 4, G1 = 4 and F1 = 5.
And this is the “official” solution: