| View unanswered posts | View active topics |
It is currently Fri Apr 26, 2024 6:46 pm ← Back to the Calcudoku puzzle page |
|
All times are UTC + 1 hour [ DST ] |
|
|
Page 2 of 3 |
[ 27 posts ] | Go to page Previous 1, 2, 3 Next |
| Print view | Previous topic | Next topic |
Calcudoku 7×7 with undetermined numbers
| Author | Message |
|---|---|
|
Posted on: Wed Dec 24, 2014 10:37 am Posts: 10 Joined: Wed Oct 15, 2014 12:42 pm |
There are 3 solutions: 181, 124 and 421 but this is not helping.
|
|
|
|
|
Posted on: Thu Dec 25, 2014 3:05 pm Posts: 57 Joined: Sun Feb 03, 2013 3:25 am |
sica wrote: There are 3 solutions: 181, 124 and 421 but this is not helping. In each of your versions are 3 numbers and this is for this calcudoku too much. Attention, this is very unusual innovation but still with no more than 1 solution… |
|
|
|
|
Posted on: Thu Dec 25, 2014 10:04 pm Posts: 10 Joined: Wed Oct 15, 2014 12:42 pm |
I wrote the numers in order from cells a1, a2 and b2. I didn't write b1=2 because it was compulsory.
|
|
|
|
|
Posted on: Thu Dec 25, 2014 10:26 pm Posts: 84 Joined: Fri May 13, 2011 9:37 am |
kozibrada wrote: sica wrote: There are 3 solutions: 181, 124 and 421 but this is not helping. In each of your versions are 3 numbers and this is for this calcudoku too much. Attention, this is very unusual innovation but still with no more than 1 solution… You are speaking of the 8^ cage? I tried all 56 combinations of sets of figures. Still the 1 solution I found remained. So the operator in this cage does not matter. |
|
|
|
|
Posted on: Fri Dec 26, 2014 3:28 pm Posts: 10 Joined: Wed Oct 15, 2014 12:42 pm |
nicow wrote: kozibrada wrote: sica wrote: There are 3 solutions: 181, 124 and 421 but this is not helping. In each of your versions are 3 numbers and this is for this calcudoku too much. Attention, this is very unusual innovation but still with no more than 1 solution… You are speaking of the 8^ cage? I tried all 56 combinations of sets of figures. Still the 1 solution I found remained. So the operator in this cage does not matter. The solution was for the 2x2 calcudoku from post 10. Yes it helps solving the 8^ cage (1 on column a, 8 and any other number on column b. But this does not help solving the main problem (written in post 8). Merry Christmas! |
|
|
|
|
Posted on: Sat Dec 27, 2014 2:02 am Posts: 84 Joined: Fri May 13, 2011 9:37 am |
The main problem is the large 3| cage. It must be filled with {0,1,2,3}, but then some other operator must be faulty.
|
|
|
|
|
Posted on: Sat Dec 27, 2014 8:55 pm Posts: 57 Joined: Sun Feb 03, 2013 3:25 am |
I try to show you “certain” steps, and indeed the way to the unique solution.
Black: evident numbers/combinations; following orange, blue, green and red… 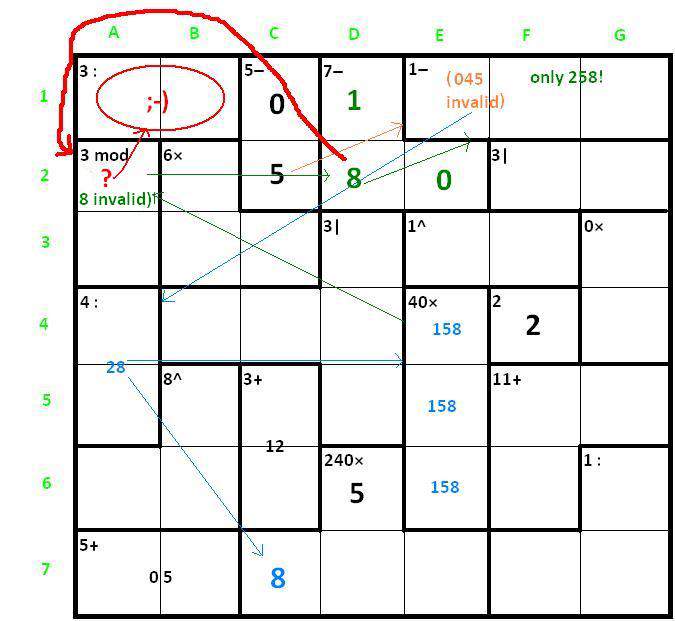 Last edited by kozibrada on Fri Jan 12, 2018 5:17 am, edited 1 time in total. |
|
|
|
|
Posted on: Sat Dec 27, 2014 10:56 pm Posts: 10 Joined: Wed Oct 15, 2014 12:42 pm |
Very nice solution.
I found another solution (for row 1 and 2). But the real problem is on row 3. |
|
|
|
|
Posted on: Sat Dec 27, 2014 11:43 pm Posts: 38 Joined: Mon May 05, 2014 4:59 am |
kozibrada wrote: sica wrote: There are 3 solutions: 181, 124 and 421 but this is not helping. In each of your versions are 3 numbers and this is for this calcudoku too much. Attention, this is very unusual innovation but still with no more than 1 solution… The only solution I can see is if you've allowed the use of duplicate numbers. So the solution to the 2x2 you posted would be [2, 2]; [2, 2]. That's the only thing that makes this puzzle make sense for me. |
|
|
|
|
Posted on: Sun Dec 28, 2014 12:59 am Posts: 57 Joined: Sun Feb 03, 2013 3:25 am |
firefly wrote: The only solution I can see is if you've allowed the use of duplicate numbers. So the solution to the 2x2 you posted would be [2, 2]; [2, 2]. That's the only thing that makes this puzzle make sense for me. ![RollEyes [rolleyes]](./images/smilies/msp_rolleyes.gif) Now it makes sense in relation to the “7×7” (already possible to see in my today’s sketch)… |
|
|
|
|
|
Page 2 of 3 |
[ 27 posts ] | Go to page Previous 1, 2, 3 Next |
|
All times are UTC + 1 hour [ DST ] |
| You cannot post new topics in this forum You cannot reply to topics in this forum You cannot edit your posts in this forum You cannot delete your posts in this forum |