| View unanswered posts | View active topics |
It is currently Thu Apr 25, 2024 1:18 am ← Back to the Calcudoku puzzle page |
|
All times are UTC + 1 hour [ DST ] |
|
|
Page 2 of 4 |
[ 32 posts ] | Go to page Previous 1, 2, 3, 4 Next |
| Print view | Previous topic | Next topic |
Trial and error
| Author | Message |
|---|---|
|
Posted on: Fri Sep 23, 2011 11:29 am Posts: 3304 Joined: Thu May 12, 2011 11:58 pm |
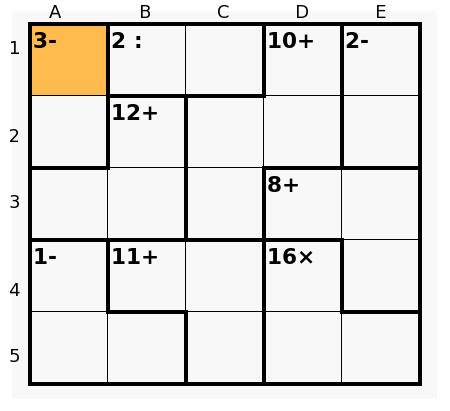
pnm wrote: I think the 5x5 difficult is almost always solvable with analysis (someone correct me if I'm wrong..), simply because it's such a small puzzle. Just did the 5x5, and yes, definitely doable... For example, to get started, by considering the combinations for the 1- cage at the bottom left, and the 16x cage at the bottom right, you can figure out quite easily that there should be a 3 in C5. Which gives you the whole 11+ cage. Then try to infer what has to go into E4. Then consider what the options are for the 8+ cage, and for the 12+ cage in the same row, and figure out what the solution is for C3. etc. etc... 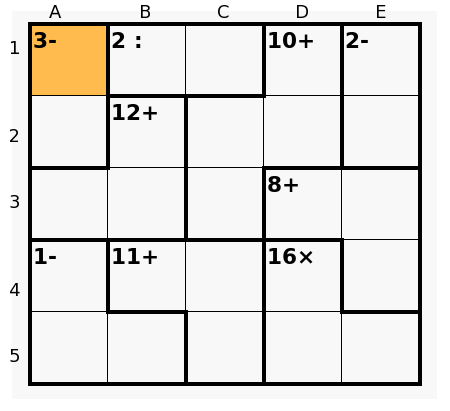 |
|
|
|
|
Posted on: Sun Oct 02, 2011 8:18 pm Posts: 116 Joined: Sat May 14, 2011 3:18 am |
pnm wrote: Given that the 16x could be either 4x1x4 or 2x4x2 and that 1- could be either 5-3-1, 5-2-2, or 4-2-1 (each in various combinations within the cage), I fail to see how "you can figure out quite easily that there should be a 3 in C5." To me, it looks like a lot of trial and error just to get to that point. Also, earlier in this thread a couple of people mention "parity checks." What is that, and how do you use it to solve calcudoku? |
|
|
|
|
Posted on: Sun Oct 02, 2011 9:32 pm Posts: 3304 Joined: Thu May 12, 2011 11:58 pm |
pharosian wrote: Given that the 16x could be either 4x1x4 or 2x4x2 and that 1- could be either 5-3-1, 5-2-2, or 4-2-1 (each in various combinations within the cage), I fail to see how "you can figure out quite easily that there should be a 3 in C5." To me, it looks like a lot of trial and error just to get to that point. Well, yes, you 're right, you would have to try those combinations. pharosian wrote: Also, earlier in this thread a couple of people mention "parity checks." What is that, and how do you use it to solve calcudoku? Check out clm's thread on "the parity" Patrick |
|
|
|
|
Posted on: Mon Oct 03, 2011 12:34 am Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
pnm wrote: pharosian wrote: Given that the 16x could be either 4x1x4 or 2x4x2 and that 1- could be either 5-3-1, 5-2-2, or 4-2-1 (each in various combinations within the cage), I fail to see how "you can figure out quite easily that there should be a 3 in C5." To me, it looks like a lot of trial and error just to get to that point. Well, yes, you 're right, you would have to try those combinations. pharosian wrote: Also, earlier in this thread a couple of people mention "parity checks." What is that, and how do you use it to solve calcudoku? Check out clm's thread on "the parity" Patrick A quick way to see this: Although the combination 3-1-1 is also possible for the cage 1-, it is rapidly supressed since 16x should be 2-4-2 and now the total known sum would be 5 + 11 + 8 = 24 so a 6 (30 - 24 to complete 2 rows) would go to E4. Then, if a 3 is inside the cage -1, the other two numbers must be 1 and 5 necessarily and now 9 + 11 = 20 and the sum of 16x and the cell E4 equals 10, but 2-4-2 and a 2 in E4 is not possible and 4-4-1 and a 1 in E4 go against the hypothesis (because in this case two 1's have already been considered present in rows 4 and 5). So the 3 must go to C5. (and, inmediately, B4 = 3, C4 = 5). Also we see that 2-4-2 is not valid in 16x since 5-1 in A5-B5 produce a 3 in A4,... , concluding that 16x = 4-1-4 and then 5-2-2 for the cage 1-, etc.). But perhaps the fastest way is: To consider only 3-1-1 (as before), supressing this combination, and since 4-2-1 is not possible (two 4's in case of 4-1-4 or two 2's in case of 2-4-2), the other possibilities 5-3-1 or 5-2-2 have a sum of 9, so the sum of 16x and E4 equals 10, then 2-4-2 is not valid (E4 = 2) so 16x = 4-1-4 and E4 = 1, and now two 1's in rows 4 and 5 drive to 1- = 5-2-2 (and not 5-3-1). Rows 4 and 5 are totally defined. For the question of the parity, and using this same diagram: The sum of the whole puzzle is odd (5 x 15 = 75). Every two cages odd produce a sum of all numbers inside them even (for instance the cages 1- and 11+); 2- we know is an even cage, and since 3- is odd, finally the addition of the cages 2: and 16x must be even, but now we know that 16x is odd (4-1-4) so 2: must be odd too and then 1-2 is the only valid combination (not 2-4); we can write the pair 1-2 as the final candidates in B1-C1 inmediately after solving the cage 16x. Thanks, Patrick, for the reference to my original post, in that moment I did not provide a diagram showing a good example of the use of this property, but anyway the target is understanding the nuclear idea. |
|
|
|
|
Posted on: Tue Oct 04, 2011 3:56 pm Posts: 116 Joined: Sat May 14, 2011 3:18 am |
Thanks, clm!
I have since read your article on parity. I'm still trying to get used to thinking about cages in these terms, but I see how it could be helpful. Of more immediate assistance, however, is your comment about keeping the sum of the rows (or columns) in mind. I use a sum on each row and column when I'm using Excel to solve book puzzles, but it's always been more of a "sanity check" to ensure that my solution doesn't have dupes in a row or column because my Excel spreadsheet doesn't have Patrick's handy "continuous checking" property to flag errors. I see now, though, that if I keep the sum in mind as you describe in your first sentence, I could rule out possibilities more quickly. |
|
|
|
|
Posted on: Tue Oct 11, 2011 7:23 pm Posts: 246 Location: Lisbon, Portugal Joined: Sun Sep 18, 2011 5:40 pm |
Patrick, the 5x5 difficult of today (11OCT11) I only "analysed" the row 5 :
34,34,125,125,125 After that, it is impossible ( for me ) to continue the solution without the Trial and Error. Did I fail anything or are there any of those little puzzles only solved with Trial and Error? |
|
|
|
|
Posted on: Tue Oct 11, 2011 8:08 pm Posts: 3304 Joined: Thu May 12, 2011 11:58 pm |
jomapil wrote: After that, it is impossible ( for me ) to continue the solution without the Trial and Error. Did I fail anything or are there any of those little puzzles only solved with Trial and Error? The way I'd continue would be along these lines: - the 1- in e1,e2,e3 can only be 4,1,2 or 5,1,3 - so the number in e5 has to be a 2 or a 5 - so the number in e4 has to be a 3 or a 4 - so the 8+ cage must have a 3 somewhere then: - the 2- cage in a3,a4,b4 can only be 4,1,1 or 5,1,2 - the 11+ cage can only be 2,4,5 or 5,1,5 (3,5,3 not possible because of the 3 in the 8+ cage) - but 5,1,5 also impossible, because then the 2- cage should be 4,1,1 - so the 11+ cage must have 2,4,5 then: - the 2- cage cannot be 4,1,1 because then the left column would have 4,1,3, leaving 2,5 for the 2- cage at the top left so: - the 8+ cage cannot have 2,3 in d3 and d4 - so a 1 has to go into c5 etc. etc. I'll leave it to others to finish the story Patrick |
|
|
|
|
Posted on: Tue Oct 11, 2011 10:50 pm Posts: 428 Location: Canada Joined: Fri May 13, 2011 2:43 am |
I did it more like this:
- after 3,4 and 1,2,5 in row 5... - a3,a4,b4 has to be 1,1,4 or 1,2,5 - it cannot be 1,1,4 because then a5,b5 would be 3,4 which only leaves 2 and 5 to go into the 2- cage at a1,a2 - so a3,a4,b5 must be 1,2,5 - then sum row 3 and 4 = 1+2+5+11+8+e3 = 30 so e3=3 - e1,e2,e3 can only be 1,3,5 with e3=3 - then e5=2, e4=4 - then d3, d4 must be 1,3 with d3=1, d4=3 - then d5=5, c5=1 - then d1,d2 must be 4,2 so c1=3 - since solutions are unique, a1,a2 cannot be 2,4 so there must be a2=3 - then a5=4, b5=3 - there can only be 5,2,2 or 3,1,1 or 4,1,2 or 5,1,3 in 1- L-shaped cage so b1,b2,c2 must be 4,1,2 or 5,1,3 (must have a 1) - so a1=5, e1=1, e2=5, a3=2, a4=1, b4=5 - then b1,b2,c2 must be 4,1,2 - since solutions are unique, b2=1 - then b1=2, b3=4, c2=4, c3=5, c4=2 DONE Lots of other ways to arrive at solution... |
|
|
|
|
Posted on: Tue Oct 11, 2011 10:56 pm Posts: 3304 Joined: Thu May 12, 2011 11:58 pm |
sneaklyfox wrote: I did it more like this: - after 3,4 and 1,2,5 in row 5... ... - then b1=2, b3=4, c2=4, c3=5, c4=2 DONE This shows why you're always faster than me |
|
|
|
|
Posted on: Tue Oct 11, 2011 11:11 pm Posts: 246 Location: Lisbon, Portugal Joined: Sun Sep 18, 2011 5:40 pm |
I never performed an analysis in that way. It looks like it is appropriate for little puzzles. With 3 weeks as a calcudolic I conclude the resolution of a 5x5 puzzle is a little different that a 9x9 or a 12x12, though the principles are the same.
Thank you Patrick and sneaklyfox for the lesson. |
|
|
|
|
|
Page 2 of 4 |
[ 32 posts ] | Go to page Previous 1, 2, 3, 4 Next |
|
All times are UTC + 1 hour [ DST ] |
| You cannot post new topics in this forum You cannot reply to topics in this forum You cannot edit your posts in this forum You cannot delete your posts in this forum |