The solution of a 6x6 and a 9x9 puzzles with "strange cages"
| Author |
Message |
pnm 
Posted on: Mon Nov 14, 2011 6:04 pm
Posts: 3301
Joined: Thu May 12, 2011 11:58 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca Wrt. the 9x9: I stopped my solver after one hour, after which about 22 x 10^9 possible solutions had been tried (testament to the poor quality of my solver  I'm thinking the 9x9 is too "open ended", and most likely completely unsolvable by a human (unless there's some key solving technique that I'm missing) Patrick
|
|

|
 |
pnm 
Posted on: Mon Nov 14, 2011 7:18 pm
Posts: 3301
Joined: Thu May 12, 2011 11:58 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca My solver took half an hour to compute all solutions for the 6x6.
It found 6492 solutions.
The difficulty rating is 183.
Here are a few solutions:
465123
126345
342561
514632
231456
653214
645123
326541
214635
563412
431256
152364
542163
326541
614325
453612
231456
165234
142635
326541
465312
654123
231456
513264
(these were solution number 10, 100, 1000, and 6492 found)
Patrick
|
|

|
 |
clm 
Posted on: Mon Nov 14, 2011 10:50 pm
Posts: 856
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca pnm wrote: In addtion, I like to reduce typing as much as possible
Note that in my suggested format:
6
31,+,a1b1c1a2c2a3b3c3
I could reduce it still by one character by defining:
6
+31,a1b1c1a2c2a3b3c3
(Also note that for the single cage you wrote:
2,b2
and as a result, I had to add a special case to the converter such that
it detects an operator is missing..)
And note the typing overhead for your specification:
"31+" (a1-b1-c1-a2-c2-a3-b3-c3);
- quotes
- parentheses
- dashes
- a space
- a semicolon at the end...
Granted, the dashes make the cell list a bit more readable.
Patrick It was only a suggestion (to make compatible both things), I see the difficulties, and in fact a more concise expressions are much better for the solver, you are right, but I was thinking that you could implement "any" expression. Well, your text form is an easy and convenient way to avoid graphics and be able to quickly transmit you some puzzle configuration from time to time (by the way, yes, I did not notice that the + was required for the single cells too). For my new "international terminology" it would be necessary to create a totally new compiler (in case of translating that language to a representation, for instance...). But we are talking about two different things in fact because the idea of the "terminology" is more to have a tool to explain the full process of the solution of a puzzle, or part of the process, etc.. I am thinking now in prepearing examples of the solutions of the puzzles using the PowerPoint, will see..., that gives better quality than the video transmisions, undoubtedly, and it would permit the players to advance very slowly just by clicking the keyboard, etc., at that time the insertion of the notes could be in this "international terminology" and not in English, Spanish or any other language (of course it would be necessary to insert a "reference" to that language with a call to the Forum of the www. calcudoku.org; the PowerPoint permits additionally to add the voice in any language).
|
|

|
 |
clm 
Posted on: Mon Nov 14, 2011 11:38 pm
Posts: 856
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca pnm wrote: Wrt. the 9x9: I stopped my solver after one hour, after which about 22 x 10^9 possible solutions had been tried (testament to the poor quality of my solver  I'm thinking the 9x9 is too "open ended", and most likely completely unsolvable by a human (unless there's some key solving technique that I'm missing) Patrick Very curious. If a 6x6, even knowing the exact compostion of the cages, has 6492 solutions (by spinning those numbers around the central "hole" of the cages and combining the 4 cages to a valid grid) (I suppose excluding symmetries), how many a 9x9 would have?. The number of different diagrams (excluding symmetries), just the "configuration", before stablishing the cages, that is, the restrictions, is 3 for a 3x3 (with the 1's in the diagonal, the 2's in the diagonal and the 3's in the diagonal); for the 4x4 I think is 108 (in three classes, 36 with one pair of equal corners, 36 with two pairs of equal corners, and 36 with all four corners different), etc. The number of valid grids grows almost "in vertical" and we know the very high number, 6,671 x 10 ^ 21 of valid "sudoku grids" (9x9). The case of the 6x6: with a rating of 183 it would be solvable by a human, even if the solution is not unique (one of those 6492), the program could return the "congratulations"; perhaps you may introduce some type of complementary (additional challeging puzzles), without points, without time limitation (neither 24 hours or 72 hours...) and just indicate (without names) "solved by 12 puzzlers..." and after some time, a month or so, put new ones, just for hobby.
|
|

|
 |
pnm 
Posted on: Tue Nov 15, 2011 12:12 am
Posts: 3301
Joined: Thu May 12, 2011 11:58 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca clm wrote: perhaps you may introduce some type of complementary (additional challeging puzzles), without points, without time limitation (neither 24 hours or 72 hours...) and just indicate (without names) "solved by 12 puzzlers..." and after some time, a month or so, put new ones, just for hobby. What I should introduce is a "user puzzle" feature: simply upload a file in that format, and it becomes a puzzle created by clm. The solver would assign points to it based on difficulty level, etc... Patrick
|
|

|
 |
clm 
Posted on: Tue Nov 15, 2011 12:17 am
Posts: 856
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca pnm wrote: Wrt. the 9x9: I stopped my solver after one hour, after which about 22 x 10^9 possible solutions had been tried (testament to the poor quality of my solver  I'm thinking the 9x9 is too "open ended", and most likely completely unsolvable by a human (unless there's some key solving technique that I'm missing) Patrick Perhaps there are not many solutions and because of the high number of combinations in the case of the 9x9 it would have required more time to find the first solution. Here is the solution: 
|
|

|
 |
beaker 
Posted on: Tue Nov 15, 2011 1:59 am
Posts: 931
Location: Ladysmith, BC, Canada
Joined: Fri May 13, 2011 1:37 am

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca This kenken is beyond my ken ![Confused [confused]](./images/smilies/msp_confused.gif)
|
|

|
 |
clm 
Posted on: Tue Nov 15, 2011 12:37 pm
Posts: 856
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca pnm wrote: My solver took half an hour to compute all solutions for the 6x6.
It found 6492 solutions.
The difficulty rating is 183.
Here are a few solutions:
465123
126345
342561
514632
231456
653214
645123
326541
214635
563412
431256
152364
542163
326541
614325
453612
231456
165234
142635
326541
465312
654123
231456
513264
(these were solution number 10, 100, 1000, and 6492 found)
Patrick Now, knowing that there are 6492!!! solutions, it would probably be interesting looking for at least one. But, with a rating of 183, this requires some time. Here is one of those 6492 solutions: 
|
|

|
 |
pnm 
Posted on: Tue Nov 15, 2011 3:06 pm
Posts: 3301
Joined: Thu May 12, 2011 11:58 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca clm wrote: Now, knowing that there are 6492!!! solutions, it would probably be interesting looking for at least one. But, with a rating of 183, this requires some time.
What's also interesting is how to modify the puzzle so there's exactly one solution... I'm wondering if this could be programmed. The solver determines there are >= 2 solutions (determined quite quickly), and then the puzzle is modified in a way that is known to reduce the number of solutions (simple example: split a large cage into two), etc. Patrick
|
|

|
 |
clm 
Posted on: Tue Nov 15, 2011 8:38 pm
Posts: 856
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The solution of a 6x6 and a 9x9 puzzles with "strange ca pnm wrote: clm wrote: Now, knowing that there are 6492!!! solutions, it would probably be interesting looking for at least one. But, with a rating of 183, this requires some time.
What's also interesting is how to modify the puzzle so there's exactly one solution... I'm wondering if this could be programmed. The solver determines there are >= 2 solutions (determined quite quickly), and then the puzzle is modified in a way that is known to reduce the number of solutions (simple example: split a large cage into two), etc. Patrick We could try your idea and see what happens, I broke (in my solution) a big cage into two parts: 6 31,+,a1b1c1a2c2a3b3c3 2,+,b2 150,x,d1d2d3e3f3 4,+,e2 2,-,e1f1f2 3600,x,a4b4c4a5c5a6b6c6 3,+,b5 28,+,d4e4f4d5f5d6e6f6 5,+,e5 Here is the graphic anyway 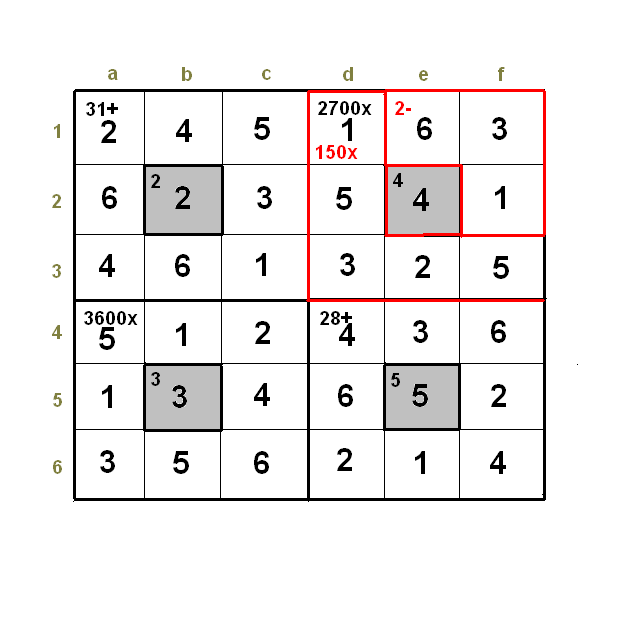
|
|

|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
|

|


![Confused [confused]](./images/smilies/msp_confused.gif)

