| View unanswered posts | View active topics |
It is currently Sat Apr 27, 2024 12:54 am ← Back to the Calcudoku puzzle page |
|
All times are UTC + 1 hour [ DST ] |
|
|
Page 1 of 3 |
[ 21 posts ] | Go to page 1, 2, 3 Next |
| Print view | Previous topic | Next topic |
Something I've always been curious about
| Author | Message |
|---|---|
|
Posted on: Wed Nov 16, 2011 11:38 am Posts: 212 Joined: Fri May 13, 2011 2:11 am |
http://www.calcudoku.org/en/2011-11-15/6/3
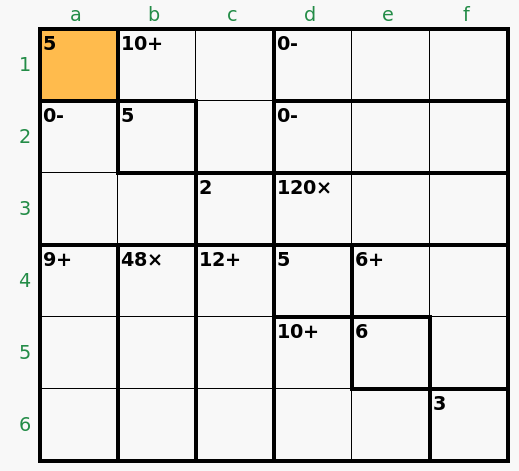 In puzzles like this one, as a rule, must one of the e4-f4-f5 and d5-d6-e6 cages be a cage of the form x-y-x? That is, in this particular one the e4-f4-f5 cage is 1-4-1. Is this an actual rule or something that has just coincidentally happened on every one of these I've done? |
|
|
|
|
Posted on: Fri Nov 18, 2011 1:19 am Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
starling wrote: http://www.calcudoku.org/en/2011-11-15/6/3 In puzzles like this one, as a rule, must one of the e4-f4-f5 and d5-d6-e6 cages be a cage of the form x-y-x? That is, in this particular one the e4-f4-f5 cage is 1-4-1. Is this an actual rule or something that has just coincidentally happened on every one of these I've done? Hi, starling, until Patrick answers to this subject, I have been playing a little bit with a “similar” puzzle. In my opinion it is quite difficult to make an accurate demonstration on that subject. Initially we can observe that the blue areas (and the white areas) have the same sum (30) (the white areas have a sum of 33) since they are complementary to 63 (3 lines) of the other coloured area, but this is a very poor information. However it looks like the bottom right blue area is the key for the full puzzle. This is the Puzzle id 377865, Nov15, 2011, 6x6 difficult, you refer to: 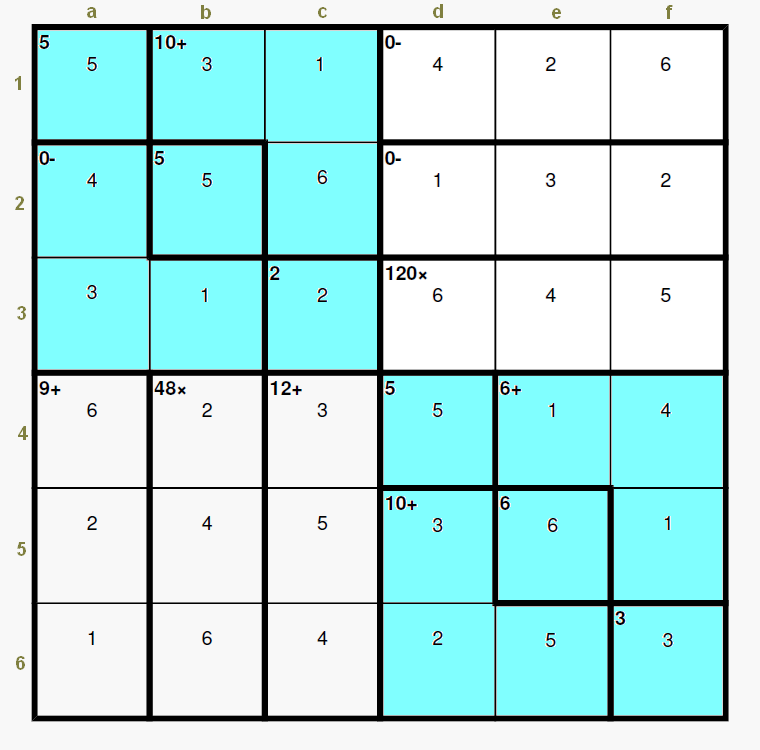 Let’s try the following example: 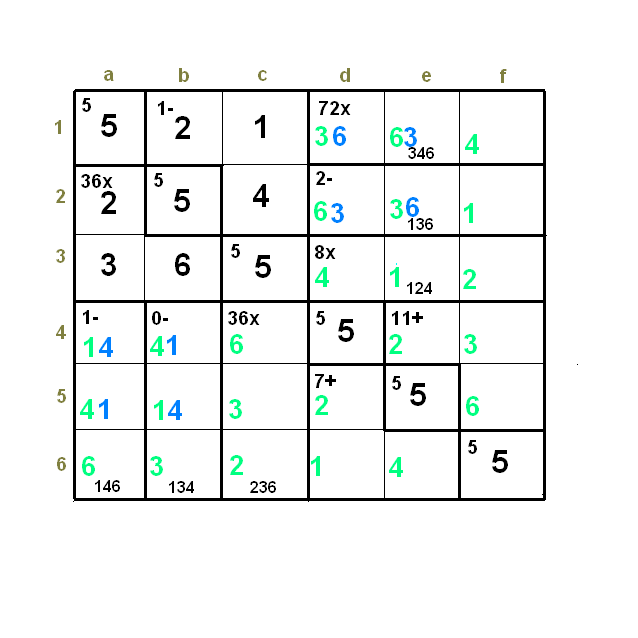 The numbers in black are clearly determined: “8x” = [1, 2, 4] ---> a3-b3 = [3, 6] ---> a2 = 2 ---> “2-“ = [1, 3, 6] ---> c2 = 4 ---> c1 = 1 ---> b1 = 2 ---> b3 = 6; a3 = 3; “1-“ (a4-a5-a6) = [1, 4, 6]; “0-“ = [1, 3, 4], the other products with only one combination. Initially the cage “11+” = [1, 4, 6], [1, 5, 5], [2, 3, 6], [2, 4, 5], [3, 3, 5], [3, 4, 4], but since neither a single 5, nor a double 3, nor a double 4 are allowed, two combinations would only be possible: [1, 4, 6] and [2, 3, 6]. Let’s start, first graphic, with this last one. In this case “7+” = [1, 2, 4] (the pending numbers in columns d, e and f). Curiously, in this case, there is some symmetrie with the content of the cages “36x” and “1-“ (b1-c1-c2). Let’s choose the sequence e4 = 2, f4 = 3, f5 = 6 (may be permuted) and d5 = 2, d6 = 1, e6 = 4 (may be permuted). In these conditions we have 4 different solutions (swapping the blue numbers, the 1’s with the 4’s, and the 3’s with the 6’s). In the second graphic 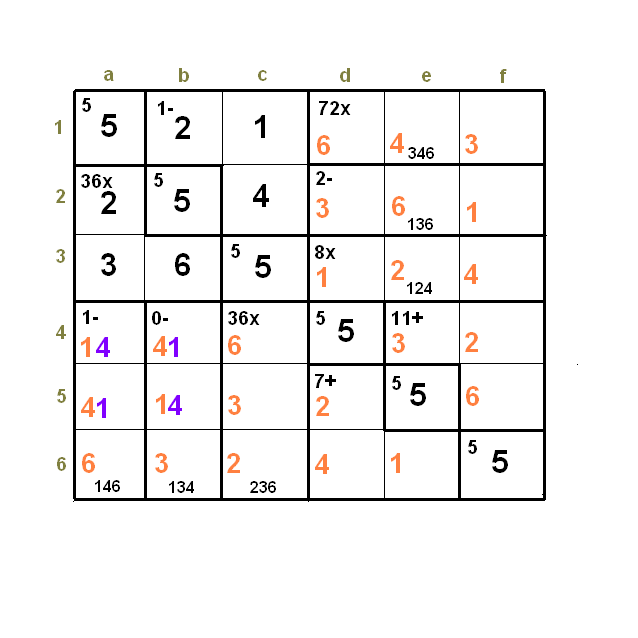 we have modified the sequence inside the cages “11+” and “7+” and we can see the two solutions swapping the 1’s and the 4’s (in indigo color). We may continue permuting the numbers inside “11+” and “7+”… Now, for the third and fourth graphics, we will use the other allowed combination for “11+”, that is, the [1, 4, 6] ---> “7+” = [2, 2, 3]. Now we see, graphic 3, that it is possible to permute the numbers in the top right area (numbers in light blue); and in the case of graphic 4, where the numbers in “11+” have a different permutation we have two solutions when permuting the 1’s and the 4’s (in violet color). So, with this puzzle, even having a cage of the type x-y-x we can not remove all uncertainties, it is not a sufficient condition, so we would need more restrictions elsewhere or simply a different configuration of all cages in order to produce a puzzle with a unique solution. 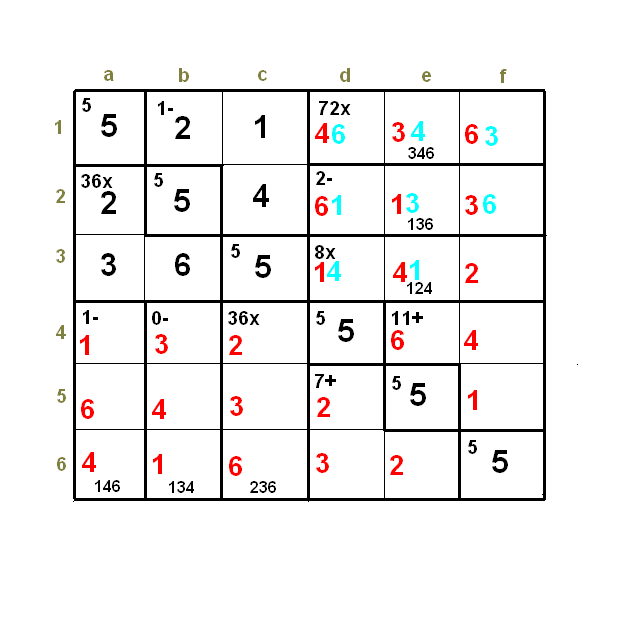  |
|
|
|
|
Posted on: Fri Nov 18, 2011 4:22 am Posts: 212 Joined: Fri May 13, 2011 2:11 am |
So given another identically cage structured puzzle, we end up with yet again another x-y-x cage in the solution.
I also seem to recall the same type thing popping up the last few puzzles of that type. Is there any actual mathematical proof, or am I just seeing this occur as a result of sample size? And thank you for posting the image, clm, I wasn't quite sure how to do that conveniently. |
|
|
|
|
Site Admin
Posted on: Fri Nov 18, 2011 11:28 am Posts: 116 Joined: Wed May 11, 2011 6:44 pm |
starling wrote: In puzzles like this one, as a rule, must one of the e4-f4-f5 and d5-d6-e6 cages be a cage of the form x-y-x? That is, in this particular one the e4-f4-f5 cage is 1-4-1. Is this an actual rule or something that has just coincidentally happened on every one of these I've done? I added the image to your post for reference. Looking at just the bottom right corner, it's easy to come up with something that fits: 5 3 2 3 6 1 2 5 3 So both the 10+ and the 6+ cage are not of the form x-y-x. (obviously I'm not looking at the rest of the puzzle) The next step would be to construct a puzzle with this cage pattern, and the numbers and cages in the bottom right as described above, with a single solution. Should be doable I think ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) Patrick |
|
|
|
|
Posted on: Mon Nov 21, 2011 3:21 pm Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
calcpnm wrote: starling wrote: In puzzles like this one, as a rule, must one of the e4-f4-f5 and d5-d6-e6 cages be a cage of the form x-y-x? That is, in this particular one the e4-f4-f5 cage is 1-4-1. Is this an actual rule or something that has just coincidentally happened on every one of these I've done? ... Looking at just the bottom right corner, it's easy to come up with something that fits: 5 3 2 3 6 1 2 5 3 So both the 10+ and the 6+ cage are not of the form x-y-x. (obviously I'm not looking at the rest of the puzzle) The next step would be to construct a puzzle with this cage pattern, and the numbers and cages in the bottom right as described above, with a single solution. Should be doable I think ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) Patrick Continuing with this problem, my intuition is that starling is right and that it is necessary to have at least a cage of the type x-y-x in the bottom right area (I am also curious waiting for the next tuesday’s 6x6 puzzle), but the precise demonstration is still far. It would be interesting to see how the computer generates a puzzle without that restriction (and a unique solution of course). I have been trying different samples in the “manual laboratory” but I could not find any argument against the starling’s hypothesis and I could not suppress the several solutions obtained permuting the numbers. Usually the top left area is solved first and quickly and the configuration in this area has "nothing to do" with the bottom right area since the puzzle is not symmetric (keeping the same aspect) in the sense that it would not be valid to rotate, for instance, 180 degrees to the right because we would obtain a different puzzle (only the cages themselves are symmetric, i.e., inside the blue areas, but not the full puzzle), we may observe that all six 3-cell in-line cages “look inside” the top left area providing, in some way, the required information, while what we could say of the bottom right area is that it is “blind” in this context. Then we will forget the symmetries of the full puzzle and work with the original configuration, the one of the graphic. In my previous post on this subject I was commenting that the top left and the bottom right areas (3x3 squared boxes, in blue) had the same sum (as the areas in white) but we can go a little further and affirm that they must contain exactly the same numbers (though composing different combinations inside the cages) (and the white areas too). It is easy to see this (though still it's a poor information): For instance, if in the bottom right area we have any number, let’s name it “n” (fm 1 thru 6) let’s say once, twice the “n” must be in the top right area (white area, to complete the three righmost columns), so the “n” must be once in the top left area (the blue area, to complete the three upper rows). If “n” is two times (or three times) in this bottom right area, reasoning identically, it must be two times (three times) in the opposite blue area and this happens with all numbers present in the bottom right area (same thing for the white areas). And from this point we must start the analysis, considering in how many ways 6 different numbers may be distributed in 9 different cells. The complete analysis is complex. Initially let’s name in general the numbers 1 to 6 with the letters a, b, c, d, e and f (this is indifferent, any letter can be any number). We could have this distribution of the nine cells: a b c d e f ------------ 3 3 3 0 0 0 distribution 1 3 3 2 1 0 0 distribution 2 3 3 1 1 1 0 distribution 3 3 2 2 2 0 0 distribution 4 3 2 2 1 1 0 distribution 5 3 2 1 1 1 1 distribution 6 2 2 2 2 1 0 distribution 7 2 2 2 1 1 1 distribution 8 Now let’s see distribution 1 (3 3 3 0 0 0): Case 1 (a diagonal in the form “\”) a b c c a b b c a This is the starling’s hypothesis. Case 2 (a diagonal in the form “/”, it’s really a symmetrie of the 3x3 blue box with respect to the vertical axis) c b a b a c a c b This is not the starling’s setting but now we have not a unique solution, for instance, we may have in the top right area this configuration d e f e f d f d e or this other one d f e e d f f e d both produce identical results for the three 3-cell in-line cages in the top right area, of course these, i.e., two configurations, for the top right area are also valid with case 1, what means that even in case 1 the starling’s condition would not be a sufficient condition. All this happened because numbers d, e and f (thrice each) are absolutely independent of numbers a, b and c in the bottom right area. Let’s see distribution 2 (3 3 2 1 0 0): Case 1 a b c c a b b d a in this case (starling’s) we may have d e f e f d f c e or f e d d f e e c f so several solutions are possible. Case 2 c b a b a c a d b, this is not starling’s (in fact it’s a symmetrie of case 1 with respect to the vertical axis) and admits the same combinations just seen for the top right area, so several solutions re possible. Case 3 d b a b a c a c b, it’s not starling’s but admits c e f e f d f d e or c f e e d f f e d, etc. In order to get final conclusions we would have to continue with the exhaustive analylisis of the other six distributions. |
|
|
|
|
Posted on: Sat Nov 26, 2011 12:37 pm Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
calcpnm wrote: starling wrote: In puzzles like this one, as a rule, must one of the e4-f4-f5 and d5-d6-e6 cages be a cage of the form x-y-x? That is, in this particular one the e4-f4-f5 cage is 1-4-1. Is this an actual rule or something that has just coincidentally happened on every one of these I've done? I added the image to your post for reference. Looking at just the bottom right corner, it's easy to come up with something that fits: 5 3 2 3 6 1 2 5 3 So both the 10+ and the 6+ cage are not of the form x-y-x. (obviously I'm not looking at the rest of the puzzle) The next step would be to construct a puzzle with this cage pattern, and the numbers and cages in the bottom right as described above, with a single solution. Should be doable I think ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) Patrick Continuing with the same problem, once more, the yesterday's Nov 25, 2011, 6x6 difficult puzzle id: 378225 looks to confirm (d5-d6-e6) the starling's hypothesis of the structures x-y-x. We must study this a little bit more. I am very interested in knowing if it would be possible to have any puzzle of these characteristics (with a unique solution) against the starling's hypothesis. 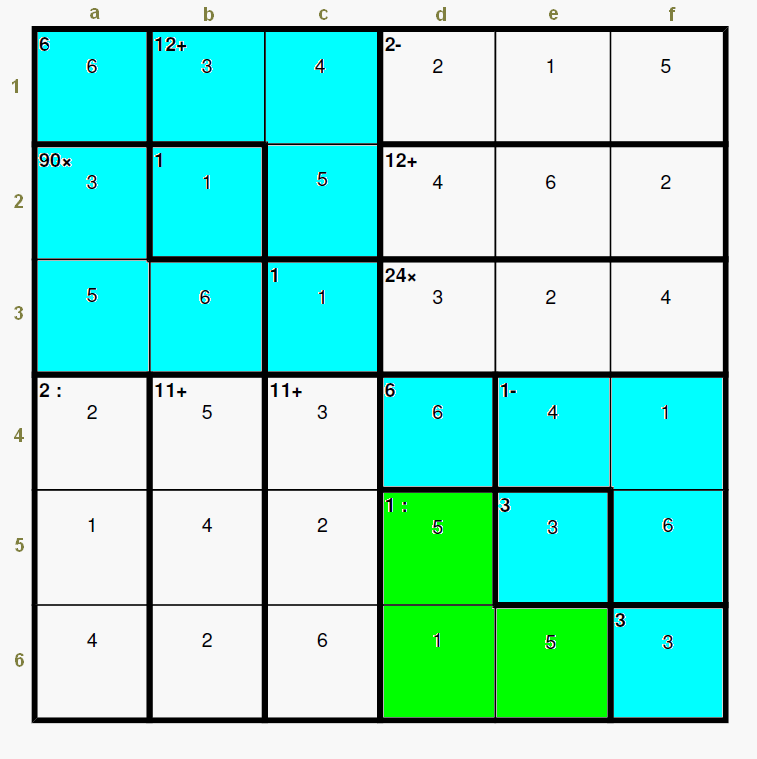 |
|
|
|
|
Posted on: Sat Nov 26, 2011 8:59 pm Posts: 931 Location: Ladysmith, BC, Canada Joined: Fri May 13, 2011 1:37 am |
All I do is the cellls and cages I'm pretty sure are right and leave the right hand lower corner alone.......then simply count the numbers of each number I've used (ie: six 6's, six 5's and so forth) to see which of the 36 numbers I'm missing and then fill in the appropriate cells to complete the last 2 cages.....or is this too simple a way to find the solution?
|
|
|
|
|
Posted on: Sun Nov 27, 2011 12:04 pm Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
beaker wrote: All I do is the cellls and cages I'm pretty sure are right and leave the right hand lower corner alone.......then simply count the numbers of each number I've used (ie: six 6's, six 5's and so forth) to see which of the 36 numbers I'm missing and then fill in the appropriate cells to complete the last 2 cages.....or is this too simple a way to find the solution? beaker, in order to solve the puzzle, your method is very good, in fact to observe the missing numbers (in rows, columns, etc... , as in the "sudokus") is one of the tools that we have, but the problem noted by starling with these 6x6 "difficult" puzzles (with this particular and special structure) is to know Why? they apparently require, in the lower right 3x3 box (this condition looks irrelevant in the upper left 3x3 box), that at least one of the two L-shape 3-cell cages have the form x-y-x, i.e., 1-4-1 on tuesday Nov 15, 5-1-5 on friday Nov 25 (perhaps for the unicity of the solution, ...), the last two 6x6's of these aspect appeared (Nov 15 and Nov 25) seem to confirm the idea of starling. It would not be easy to arrive to a full demonstration. |
|
|
|
|
Posted on: Fri Dec 16, 2011 1:22 am Posts: 212 Joined: Fri May 13, 2011 2:11 am |
Thought I should point out, yesterday's has it too, but I haven't any idea how to actually prove it has to be this way.
|
|
|
|
|
Posted on: Fri Dec 16, 2011 4:02 pm Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
starling wrote: Thought I should point out, yesterday's has it too, but I haven't any idea how to actually prove it has to be this way. I had observed that too yesterday, again a puzzle of these characteristics confirms your hypothesis, I have included the graphic for yesterdays's 6x6 Puzzle id: 392595 so we can keep the record. I am still thinking that the full demonstration will be difficult and very interesting when found. 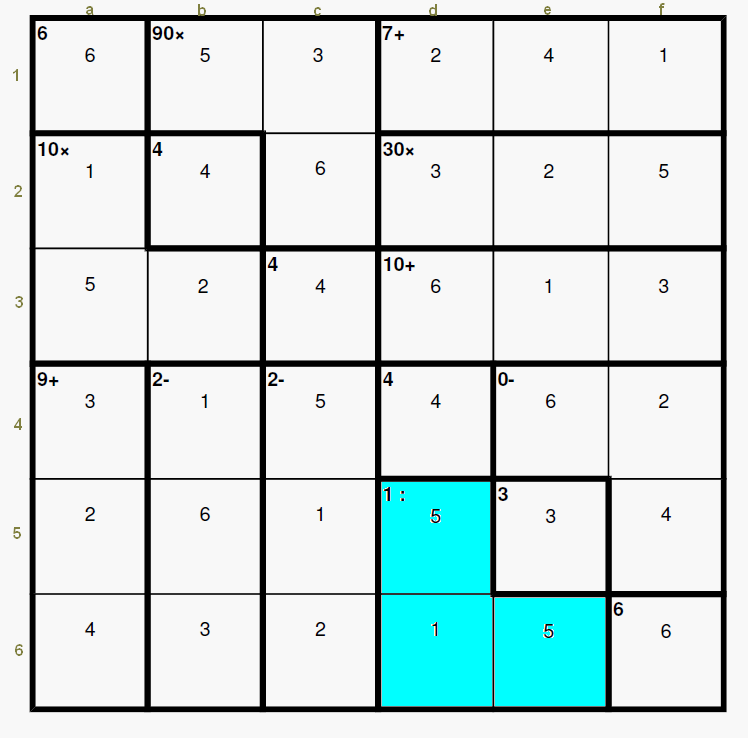 |
|
|
|
|
|
Page 1 of 3 |
[ 21 posts ] | Go to page 1, 2, 3 Next |
|
All times are UTC + 1 hour [ DST ] |
| You cannot post new topics in this forum You cannot reply to topics in this forum You cannot edit your posts in this forum You cannot delete your posts in this forum |