
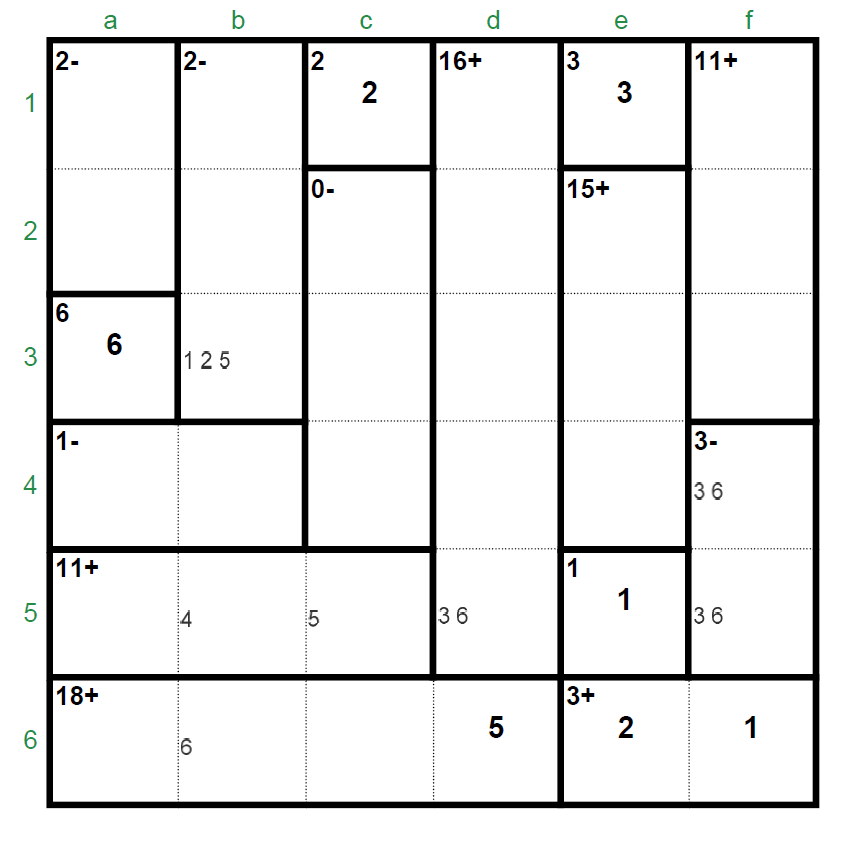
Re: help for 6x6 difficult Oct04
pluto wrote:
d6=5, e6=2, f6=1. These are obvious, but how to get further without resorting to trial and error has been bothering me off and on for several days. If anyone would care to give me a hint I'd be most appreciative. Thank you.
It is also obvious that f4-f5 = [3,6] (addition in column f) and consequently d5-f5 is also [3,6] (addition in row 5). This means that "11+" (a5-b5-c5) = [2,4,5].
Next, the only hypothesis that is really required is this: A 6 is not possible in b6 (the 6 for row 6) because >>> "2-" (b1-b2-b3) = [1,2,5] (unique) >>> b5 = 4 >>> c5 = 5 and a 6 would become impossible in column "c". Thus
c6 = 6 and, applying the parity rule to column "c",
c5 must be odd then
c5 = 5 (among 2,4,5 in cage "11+").
The rest is very simple: a5-b5 = [2,4] and a6-b6 = [3,4]. If a 1 is not in "2-" (a1-a2) it would be a4 = 1, b4 =2, "2-" (b1-b2-b3) = [1,3,6] (unique) and no 5's would be possible in column "b" so
a1 = 1,
a2 = 3 and
a4 = 5 (the 5 for column "a") >>>
b4 = 6 (being the 4's already in use in columns "a" and "b") (I am affraid this is not among your options, Patrick

). Also "2-" (b1-b2-b3) = [1,2,5] (unique, being b4 = 6).
And: b4 = 6 >>> f4 =3 >>> f5 = 6 >>> d5 = 3. The rest is completed quickly.
The graphic shows the invalid hypothesis with a 6 in b6:
 ). Also "2-" (b1-b2-b3) = [1,2,5] (unique, being b4 = 6).
). Also "2-" (b1-b2-b3) = [1,2,5] (unique, being b4 = 6).
![Sleep [sleep]](./images/smilies/msp_sleep.gif) ).
).![RollEyes [rolleyes]](./images/smilies/msp_rolleyes.gif)