| View unanswered posts | View active topics |
It is currently Wed Apr 24, 2024 9:16 am ← Back to the Calcudoku puzzle page |
|
All times are UTC + 1 hour [ DST ] |
|
|
Page 1 of 1 |
[ 8 posts ] |
| Print view | Previous topic | Next topic |
The most difficult 9x9: Fully analytical, step by step
| Author | Message |
|---|---|
|
Posted on: Mon Apr 22, 2013 12:27 pm Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
The most difficult 9x9: Full analytical solution step by step.
The Apr 02, 2013's 9x9 was considered by several players (sjs34, jaek, pnm, clm, bram, garrybl, picklepep, … ) among the more difficult puzzles appeared in this site till the moment (pse refer to thread “4/2/13 9x9” in the Section “Specific puzzles / your own puzzles”). For instance, picklepep (one of those extraordinary players) commented (Apr 08, 2013): “I just noticed that this puzzle only has a rating of 130. It's a little bit funny as it was the most difficult puzzle I've ever done”. This puzzle was finally solved by near 60 puzzlers but perhaps it’s time to develop the full solution (step by step) for a puzzle of these characteristics (I bring the solution to the Section “Solving strategies and tips”) gives us the opportunity to show some ideas and techniques (in fact we will only use the basic rules for this puzzle) that hopefully can be useful to many other players who frequently give up. And to show that we must always be confident in the “analysis” according to that old “theorem”: “If a Calcudoku has a unique solution then it can be solved using only analytical means”.  First, let’s resume here the initial discussion held in the referred thread “4/2/13 9x9”. Step 1. It's clear (applying the addition rule to the three rightmost columns with a sum of 135) that g4 + g6 = 10 >>> [2,8] or [4,6] ... but the interesting thing is that f4 + f6 = even (parity rule to the involved cages “3-” and “1-”, which sum is even, in fact f4 and f6 are both odd); since (applying now the parity rule to the three leftmost columns) c4 + c6 = odd >>> d4 + d6 = 26 - odd = odd then (parity rule for the three central columns) "60x" is odd since "378x", which is [1,6,7,9] or [2,3,7,9] (excluding the [3,3,6,7] due to the double 3), is always odd. So we have concluded that "60x" = [1,3,4,5] being invalid the combination [1,2,5,6] (and obviously excluding the [2,2,3,5] due to the double 2). Next we eliminate [4,6] for the pair g4-g6 then arriving to [2,8] and as a consequence f4 = 5. To eliminate the pair [4,6] we can do this “analysis”: Step 2. Graphic 1: Case g4 = 4 >>> f4 = 1 [now there is a 7 in “13+” (c4-d4)]. If we observe the graphic we quickly arrive to b4 = 3. In these conditions, considering the addition of the three central rows (total of 135): a + b + c = 19 (the sum of cells b6, f6 and h6); but if b = 5 >>> a + c = 14 can not be accomplished and if b = 7 >>> a + c = 12 and, as c6-d6 = [4,9], this condition can not be achieved. 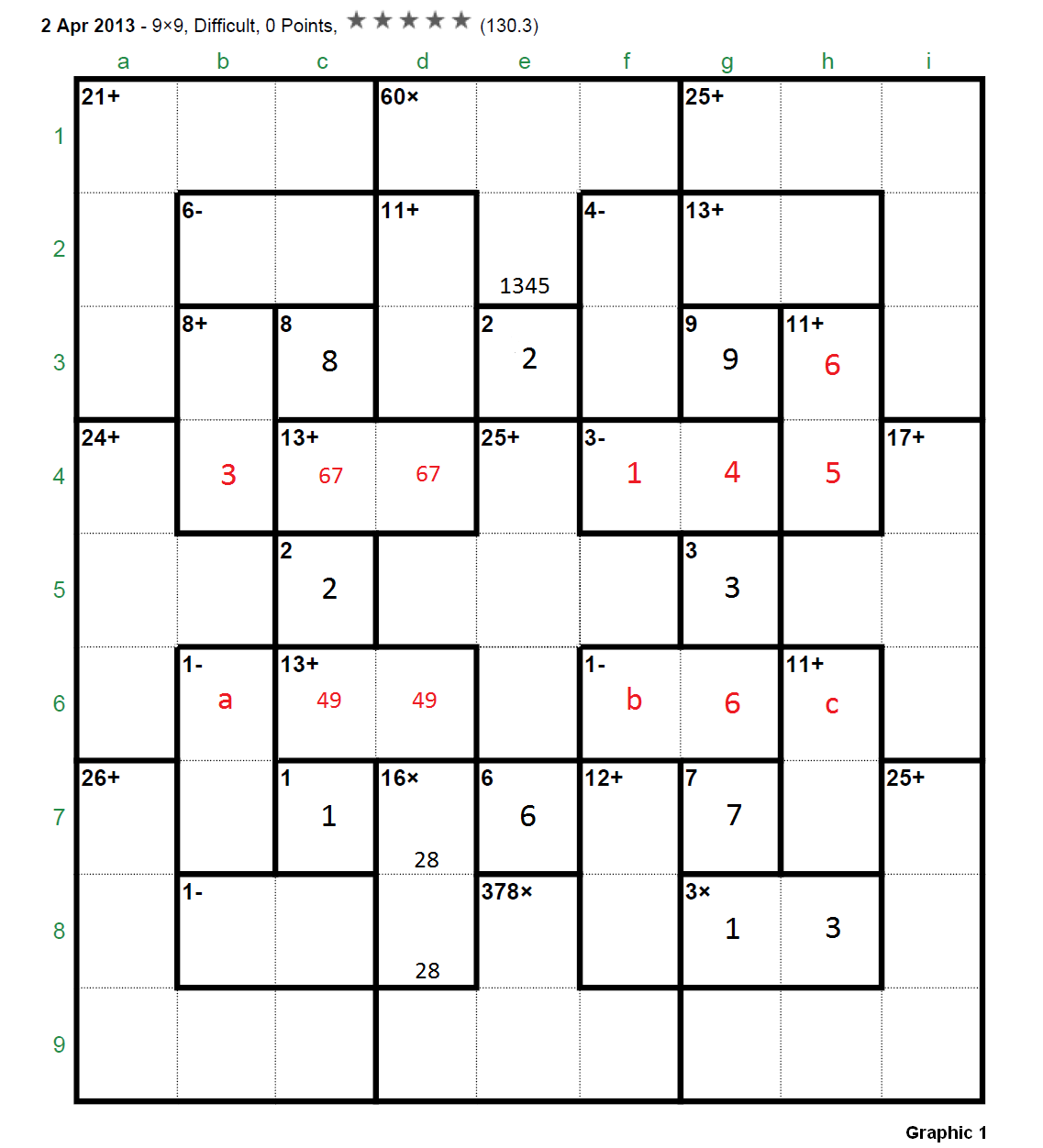 Graphic 2: Case g4 = 6 >>> f4 = 3 (c4-d4 = [4,9]) >>> f6 = 5 >>> f7-f8 = [4,8] >>> f2-f3 = [2,6] (f2 = 2; f3 = 6). The three 2’s in columns “d”, “e” and “f” (the three central columns) force “378x” = [1,6,7,9] with a sum of 23 and now, considering the addition of the three central columns (total of 135): a + b = 17 (the sum of cells d4 and d6) which is impossible due to the 8 in cage “16x”.  Step 3. Let’s observe now the Graphic 3. 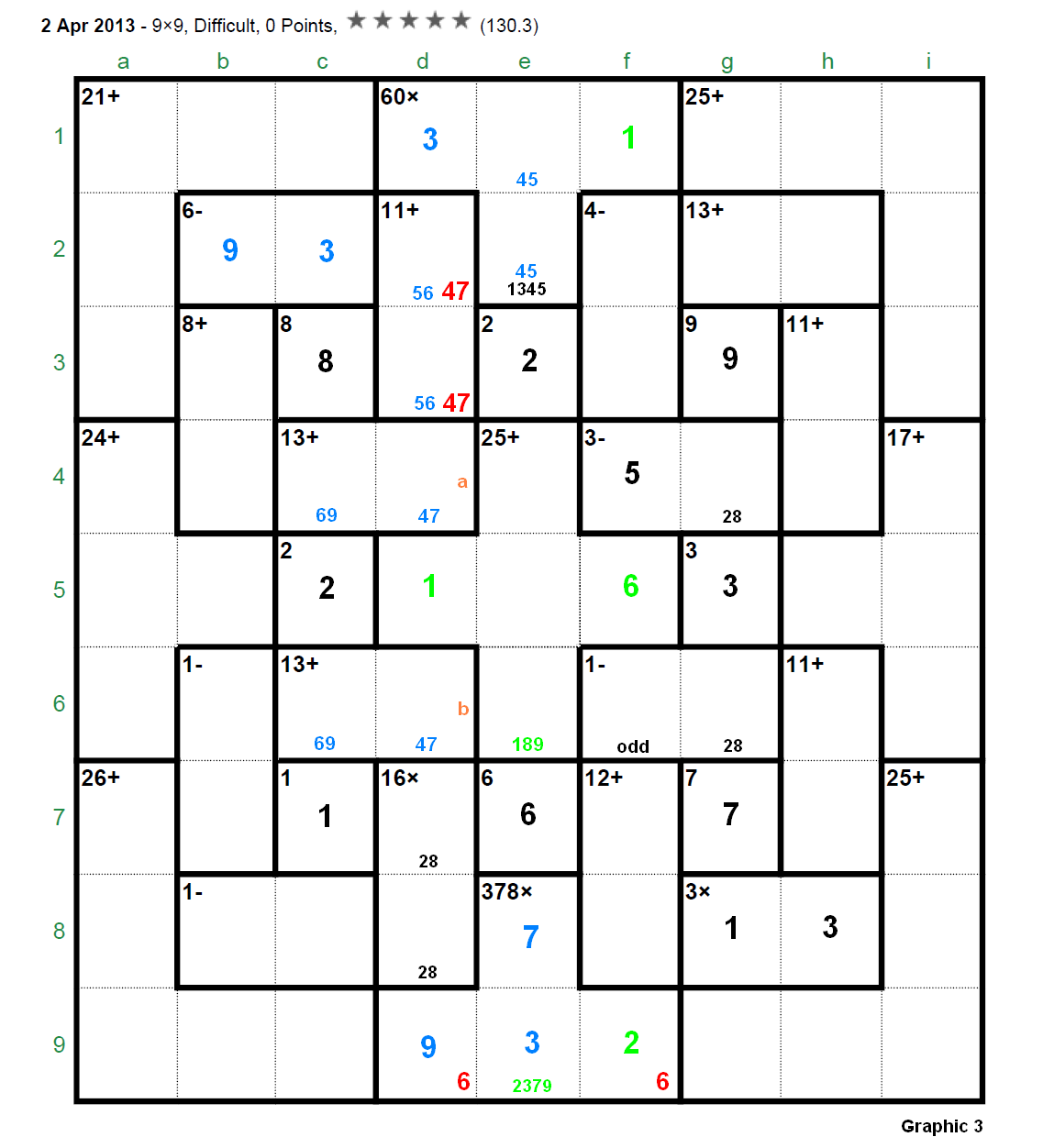 First of all we have concluded in Step 1 that d4 + d6 is odd, that is (naming these cells “a” and “b” (to “underline” them): a + b = [11,13,15] since obviously this sum, odd and different than 17, can not be 9 or lower (i.e., if this sum was 9 >>> c4 + c6 = 26 - 9 = 17 which is impossible due to c3 = 8 and a lower value produces 19 or more for c4 + c6 what is out of range). In this moment we can affirm that a 6 can not be part of “378x” according to the following: If f9 = 6 (shown in red) there is no place for a 2 in column “f” since f6 is odd and 2 is not an operand of cage “60x”; also, a 6 in d9 (shown in red) would force d2-d3 = [4,7] and it’s immediate to see that a + b could not be 11 or 13 or 15. Consequently the 6 is not part of cage “378x” >>> “378x” = [2,3,7,9] (the only left combination for this cage) and this means: f9 = 2 and now the only place for a 6 in column “f” is f5 (both shown in green colour). ********************* Remark: Observe anyway that the previous analysis to determine the combination [2,3,7,9] for the cage”378x” could have been done just after Step 1, it only depends on the fact that “60x” = [1,3,4,5] and the other arguments taken into consideration in Step 1 (often in the “analysis” the “steps” or “ways” can be interchanged). ********************* Next (in green colour): If f6 = 1 the 9 of column “f” should go to cage “12+” (= [3,9]) and then there is no place for a 7 in column “f”. This drives to f1 = 1 >>> d5 = 1 (the only place now for a 1 in column “d”). The 1 of column “e” must be in e4, e5 or e6. Since e4 + e5 + e6 = 25 - 1 - 6 = 18 >>> e4-e5-e6 = [1,8,9] (shown in green). In blue colour: A 9 in those positions force d9 = 9 and then e9 = 3 (due to h8 = 3) and e8 = 7. The 3 of cage “60x” goes to d1 and e1-e2 = [4,5]. The addition rule applied to column “d” shows that d4 + d6 = 11 and, since d6 = 5 is forbidden, it follows that d4-d6 = [4,7] >>> d2-d3 = [5,6]. Additionally c4 + c6 = 26 - 11 = 15 = [6,9]. And finally, looking to the 3’s for column “c”, it must be c2 = 3 >>> b2 = 9. Step 4 (Graphic 4, the previous final numbers or candidates shown in black colour). What would happen if we place a 2 in g6? >>> f6 = 3 (due to f1 = 1) and there is no place in column “f” for a 7, consequently: g6 = 8, g4 = 2 (in brown colour). 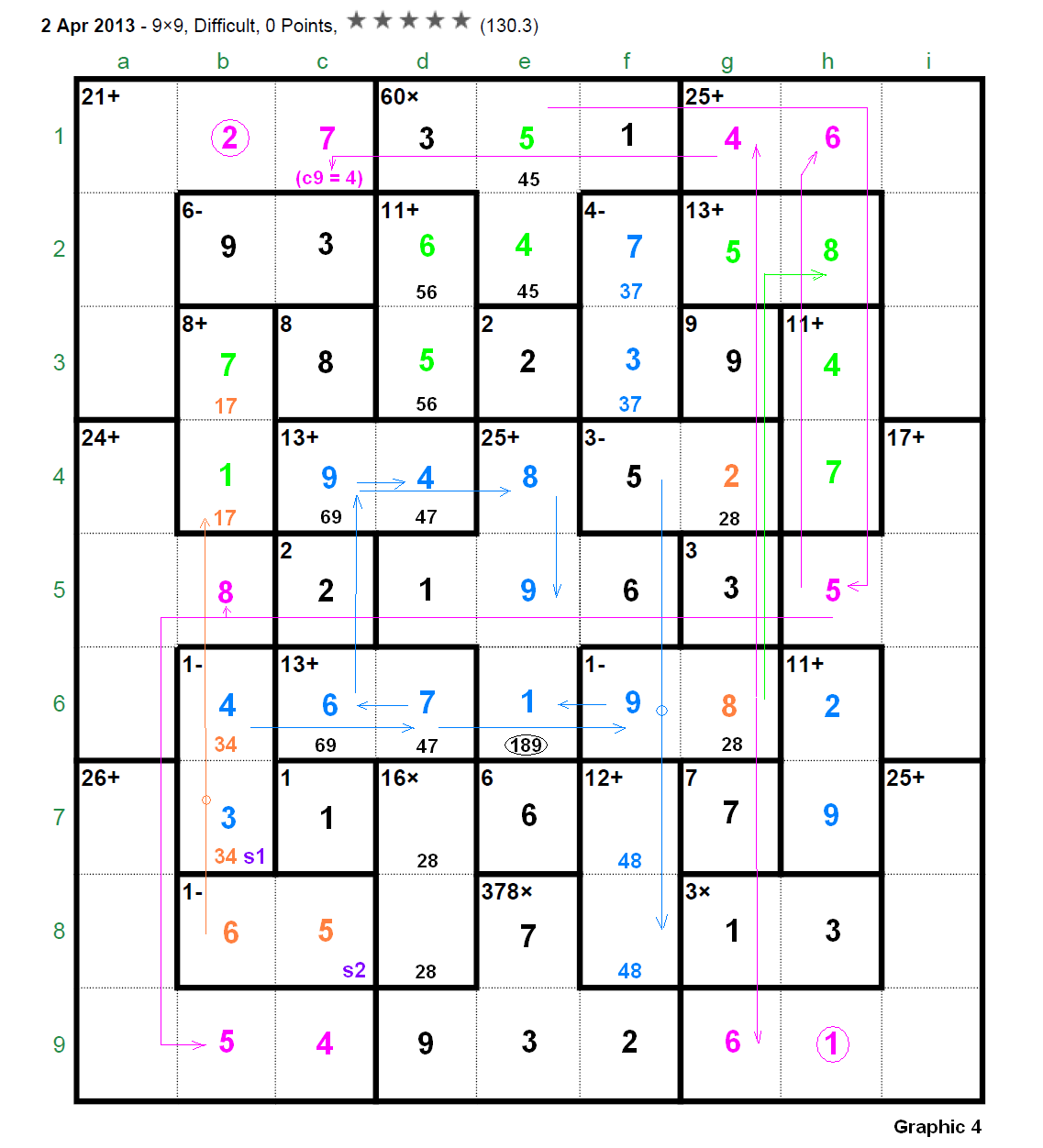 Now we work with the three leftmost columns, with a total sum of 135, the addition of cages “1-” (b6-b7) and “1-” (b8-c8) (whose sums have been named s1 and s2 in indigo colour) is 18 (135 - 21 - 12 - 8 - 8 - 24 - 15 - 2 - 26 - 1), that is, s1 + s2 = 18; since there are two 9’s in columns “b” and “c” we obtain: ”1-” (b8-c8) = [4,5], [5,6] (only two possibilities) but [4,5] is not possible due to s1 = 18 - s2 = 18 - 9 = 9 = [4,5] and two cages being simultaneously [4,5] can not occupy those positions, in a “perpendicular” shape, so necessarily “1-” (b8-c8) = [5,6]. Having already a 6 in column “c”: b8 = 6, c8 = 5; s1 = 18 - 11 = 7, that is: “1-” (b6-b7) = [3,4] and it follows that “8+” (b3-b4) = [1,7]. In this moment we move our attention to the three bottom rows, with a total sum of 135, to obtain: b7 + h7 = 12 (135 - 26 - 1 - 11 - 10 - 6 - 21 - 12 - 7 - 4 - 25) >>> b7 = 3 (b6 = 4), h7 = 9 (h6 = 2) (shown in blue colour) (otherwise b7 = 4 >>> h7 = 8 >>> h6 = 3 with a double 3 in column “h”). Step 5 (continuing with Graphic 4, in blue colour): b6 = 4 >>> d6 = 7 (c6 = 6) >>> f6 = 9 >>> e6 = 1. Also f6 = 9 and f4 = 5 >>> “12+” = [4,8] >>> “4-” = [3,7], with f2 = 7 (due to c2 = 3), f3 = 3. And, finally, c4 = 9, d4= 4; and c4 = 9 >>> e4 = 8, e5 = 9. Step 6 (continuing with Graphic 4, in green colour): We pay now attention to the three upmost rows to obtain: b3 + h3 = 11 (135 - 21 - 12 - 8 - 13 - 11 - 2 - 10 - 25 - 13 - 9). Clearly b3 <> 1 (b3 = 1 >>> h3 = 10 = out of range) so b3 = 7 (b4 = 1), h3 = 4 (h4 = 7); b2 = 9 and the 7’s in g7 and h4 drive to “13+” (g2-h2) = [5,8] with g2 = 5, h2 = 8. The 5 in g2 produces e1 = 5, e2 = 4 and d2 = 6, d3 = 5. In violet colour: If c5 = 2 and f9 = 2 we must place the 2 of column “b” in b1; if f1 = 1 and d5 = 1 the 1 of column “h” goes to h9; and e1 = 5 >>> h5 = 5 >>> h1 = 6 completing in this way column “h”. To complete column “g” is trivial because h1 = 6 >>> g9 =6, g1 = 4. If h5 = 5, going to column “b”, b9 = 5 and b5 = 8. We also complete column “c” with c1 = 7 and c9 = 4 (due to g1 = 4). Once we have arrived to this situation (Graphic 5): 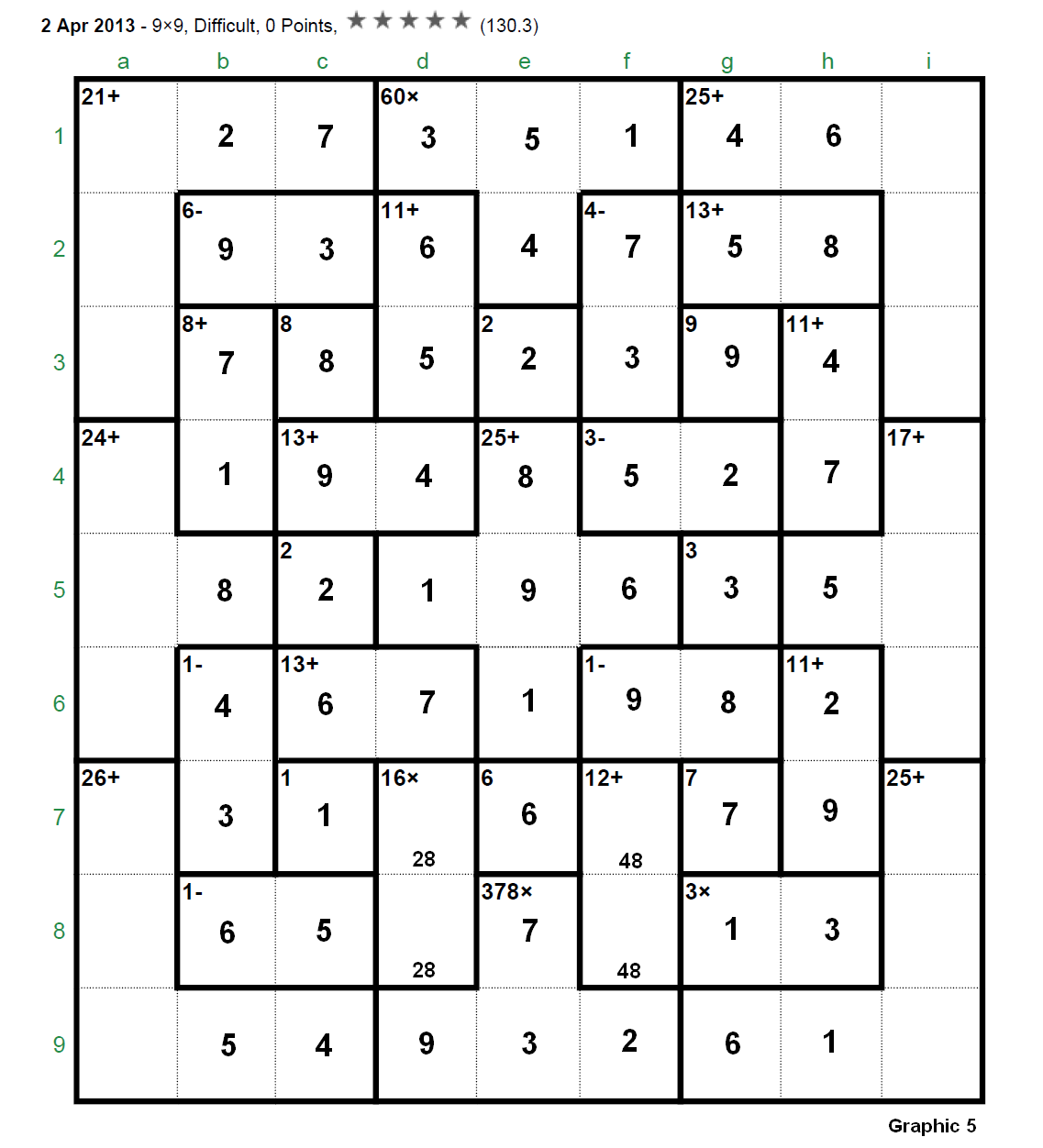 it looks very easy to finish the puzzle (only columns “a” and “i” plus the cages “16x” and “12+” have to be determined). Let’s continue anyway. Step 7 (Graphic 6, in blue colour) Let’s observe, for instance, row 6: i6 = [3,5] but if i6 = 3 >>> i4 + i5 = 9 and this situation is forbidden since [1,8], [2,7], [3,6] or [4,5] are not allowed, then i6 = 5, a6 = 3. Then in row 4: i4 = 3, a4 = 6. Also i6 = 5 >>> a7 = 5 (the 5 for row 7). Now a8 + a9 = 26 - 5 - 5 - 4 = 12 = [4,8] >>> a8 = 4, a9 = 8 and a8 = 4 >>> f8 = 8, f7 = 4; also f8 = 8 >>> d8 = 2, d7 = 8. Step 8 (in brown colour). Necessarily i9 = 7 >>> (in row 5) a5 = 7, i5 = 4. Now (in green colour): a4 = 6 >>> i3 = 6 >>> a3 = 1 >>> i2 = 1 >>> a2 = 2. And, to finish the puzzle, we enter the encircled numbers (in violet colour): a1 = 9, i1 = 8, i7 = 2, i8 = 9. And that’s all. 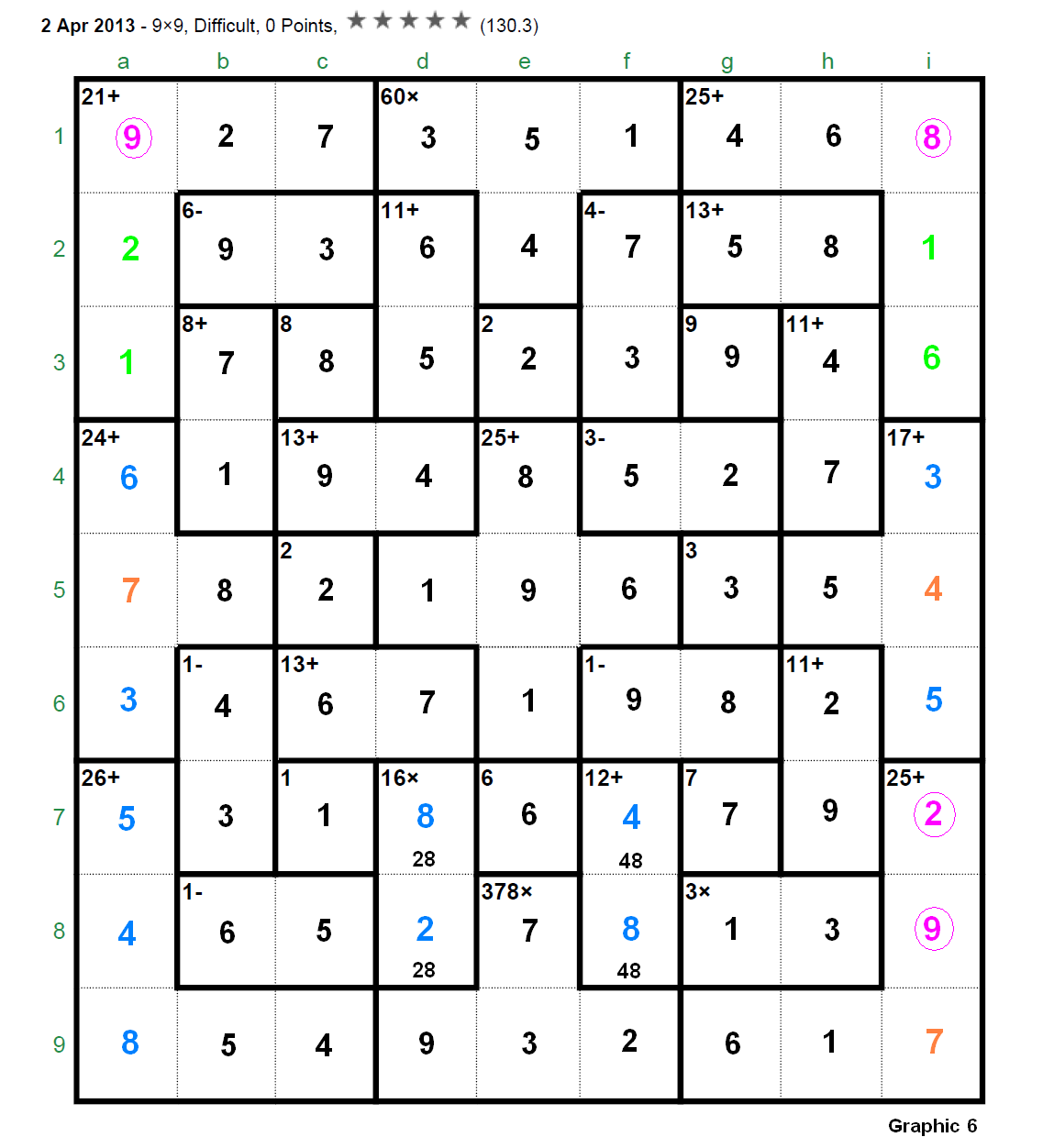 The official solution: 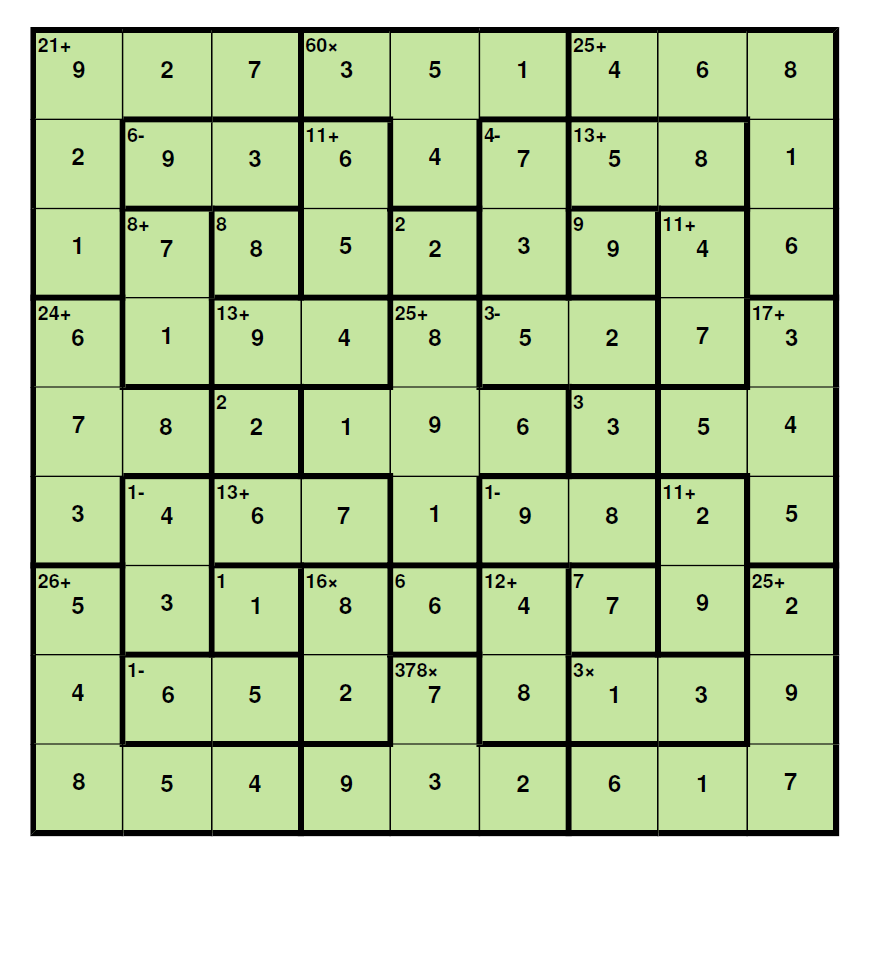 |
|
|
|
|
Posted on: Mon Apr 29, 2013 1:08 am Posts: 253 Joined: Tue May 24, 2011 4:55 pm |
clm, thank you for this most impressive, complete step-by-step demonstration! It very clearly illustrates how much can be achieved through analysis. (You may have answered this before, but which software did you use for creating the graphics?)
Remember, though, that you should never feel like you are under any kind of obligation to pour the amount of time and effort needed to make these instructive graphics into explaining the intricacies of solving advanced puzzles to the rest of us. I am saying this because I am myself trying (not too successfully so far) to go on a calcudoku hiatus as part of an effort to reclaim my real, off-screen life. Interesting as it is, calcudoku may consume a large amount of time, either because you're struggling with the hardest puzzles (like I am) or because you're kind enough to take the time needed to guide others through the maze (like you are) ![Smile [smile]](./images/smilies/msp_smile.gif) |
|
|
|
|
Posted on: Mon Apr 29, 2013 11:33 am Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
bram wrote: clm, thank you for this most impressive, complete step-by-step demonstration! It very clearly illustrates how much can be achieved through analysis. (You may have answered this before, but which software did you use for creating the graphics?) Remember, though, that you should never feel like you are under any kind of obligation to pour the amount of time and effort needed to make these instructive graphics into explaining the intricacies of solving advanced puzzles to the rest of us. I am saying this because I am myself trying (not too successfully so far) to go on a calcudoku hiatus as part of an effort to reclaim my real, off-screen life. Interesting as it is, calcudoku may consume a large amount of time, either because you're struggling with the hardest puzzles (like I am) or because you're kind enough to take the time needed to guide others through the maze (like you are) ![Smile [smile]](./images/smilies/msp_smile.gif) Thank you, bram, for your comments and interest, it´s very encouraging for me to see that there are players so patient to finish the full explanation, I always think in how to make the posts more simple, clear and attractive for the reader though sometimes, and due to the complexity of the puzzle, it's difficult to reduce at the same time the required number of graphics. I only use the program "Paint", the standard accesory provided by Windows, I just "cut" the printed (in Adobe Reader) puzzle and paste it to the "Paint" worksheet then I play on it by adding (with the standard tools) the numbers, fonts, sizes, colours, lines, etc., saving all necessary graphics (using several intermediate graphics in order to keep the previous work) in the ".png" format which occupies less memory and it's easier and faster to upload to the "ImageShack". I agree with you that it's time consuming and of very low priority (in life) but from time to time I must admit that I feel the "compulsion" to prepare one of these posts, when I have been "touché" by the extraordinary beauty of the puzzle, due to its internal structure, etc., other times just to make a modest contribution to the curiosity (that I share) of some particular player, etc., in general it's like a fight againts the computer, against the Patrick's software that, depending on the "level of difficulty", "thinks" in how to place the numbers and cages in the most difficult positions to challenge the calcudokers. And it is true that often the computer "finds" those "magic" positions!!!.  Finally I must say that one feels really good when a post like 'Full tables: "mod function" and "bitwise OR" (in the 8x8's)' (in this same section "Solving strategies and tips") has got 5,600 views what means that it's being useful to the new players. (Btw, I hope to overpass one day the most visited "Any suggestions?" in the section "Calcudoku General"). ![Smile [smile]](./images/smilies/msp_smile.gif) ![Smile [smile]](./images/smilies/msp_smile.gif) |
|
|
|
|
Posted on: Mon Apr 29, 2013 3:41 pm Posts: 276 Joined: Thu May 12, 2011 11:51 pm |
Another expression of appreciation to clm. As long as it pleases you to create your explanations, it pleases me to receive them. They are very elegant and helpful.
|
|
|
|
|
Posted on: Mon Apr 29, 2013 5:24 pm Posts: 253 Joined: Tue May 24, 2011 4:55 pm |
clm wrote: (…) Patrick's software that, depending on the "level of difficulty", "thinks" in how to place the numbers and cages in the most difficult positions to challenge the calcudokers. And it is true that often the computer "finds" those "magic" positions!!!.  Yes, it is nice that even though the puzzles are constructed by an algorithm, surprisingly often they contain a special twist somewhere that makes them look human-made. clm wrote: Finally I must say that one feels really good when a post like 'Full tables: "mod function" and "bitwise OR" (in the 8x8's)' (in this same section "Solving strategies and tips") has got 5,600 views what means that it's being useful to the new players. ![Woot [woot]](./images/smilies/msp_w00t.gif) Wow, I didn't notice that one before! But then I haven't been a frequent guest to the "Solving strategies and tips" section. Very nice work indeed and a must-read, especially for puzzlers without prior knowledge of bitwise OR. I hope it will soon reach its well-deserved Most Viewed Post Ever status Wow, I didn't notice that one before! But then I haven't been a frequent guest to the "Solving strategies and tips" section. Very nice work indeed and a must-read, especially for puzzlers without prior knowledge of bitwise OR. I hope it will soon reach its well-deserved Most Viewed Post Ever status ![ThumpUp [thumbup]](./images/smilies/msp_thumbup.gif) |
|
|
|
|
Posted on: Mon Apr 29, 2013 7:23 pm Posts: 931 Location: Ladysmith, BC, Canada Joined: Fri May 13, 2011 1:37 am |
I have been using the bitwise and mod tables since clm published them because I don't understand them (however I do now "get" the mod puzzles more easily)......I have thanked clm in the past and will now take the opportunity to thank him once more.......1/2kenken
![Smile [smile]](./images/smilies/msp_smile.gif) |
|
|
|
|
Posted on: Tue Apr 30, 2013 4:38 pm Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
sjs34 wrote: Another expression of appreciation to clm. As long as it pleases you to create your explanations, it pleases me to receive them. They are very elegant and helpful. Thank you very much for your kindness (and coming from the 6th player in the World's all time ranking!!! ... who at the same time has been enough humble to demand strategies for this specific puzzle ... ![ThumbsUp [thumbsup]](./images/smilies/msp_thumbsup.gif) ), it's very pleasant to hear that the explanations have been helpful. ), it's very pleasant to hear that the explanations have been helpful. |
|
|
|
|
Posted on: Tue Apr 30, 2013 5:08 pm Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
beaker wrote: I have been using the bitwise and mod tables since clm published them because I don't understand them (however I do now "get" the mod puzzles more easily)......I have thanked clm in the past and will now take the opportunity to thank him once more.......1/2kenken ![Smile [smile]](./images/smilies/msp_smile.gif) Thanks again, beaker. Btw, you will soon get the bitwise OR as well. It's just a question of having in mind the binary expression of the numbers 1 thru 15 and how the bitwise OR operation proceeds with every pair of bits ("keeping" them in their original positions), for instance: 3 = 0011 5 = 0101 ________ = 0111 = 7 (this is the binary expression for the number 7), that is, 3 bitwise OR 5 (or viceversa since the bitwise OR is conmutative) = 7. For the bitwise OR just operate the numbers "in vertical", considering that 0 bitwise OR 0 = 0, the other three operations produce a 1, that is, 0 bitwise OR 1 = 1; 1 bitwise OR 0 = 1 and 1 bitwise OR 1 = 1. In this way you will understand the full tables and, what is preferable, how the operation works. |
|
|
|
|
|
Page 1 of 1 |
[ 8 posts ] |
|
All times are UTC + 1 hour [ DST ] |
| You cannot post new topics in this forum You cannot reply to topics in this forum You cannot edit your posts in this forum You cannot delete your posts in this forum |