| Author |
Message |
jomapil 
Posted on: Sat Jun 09, 2012 11:17 pm
Posts: 246
Location: Lisbon, Portugal
Joined: Sun Sep 18, 2011 5:40 pm

|
 More fuel to the fire Still the controversy between " Trial And Error method " ( TAE ) and " Analytical method ". The next picture is an incomplete diagram of the puzzle 9x9 ( 16JUN2012 ). I arrived at that point with only pure analysis. 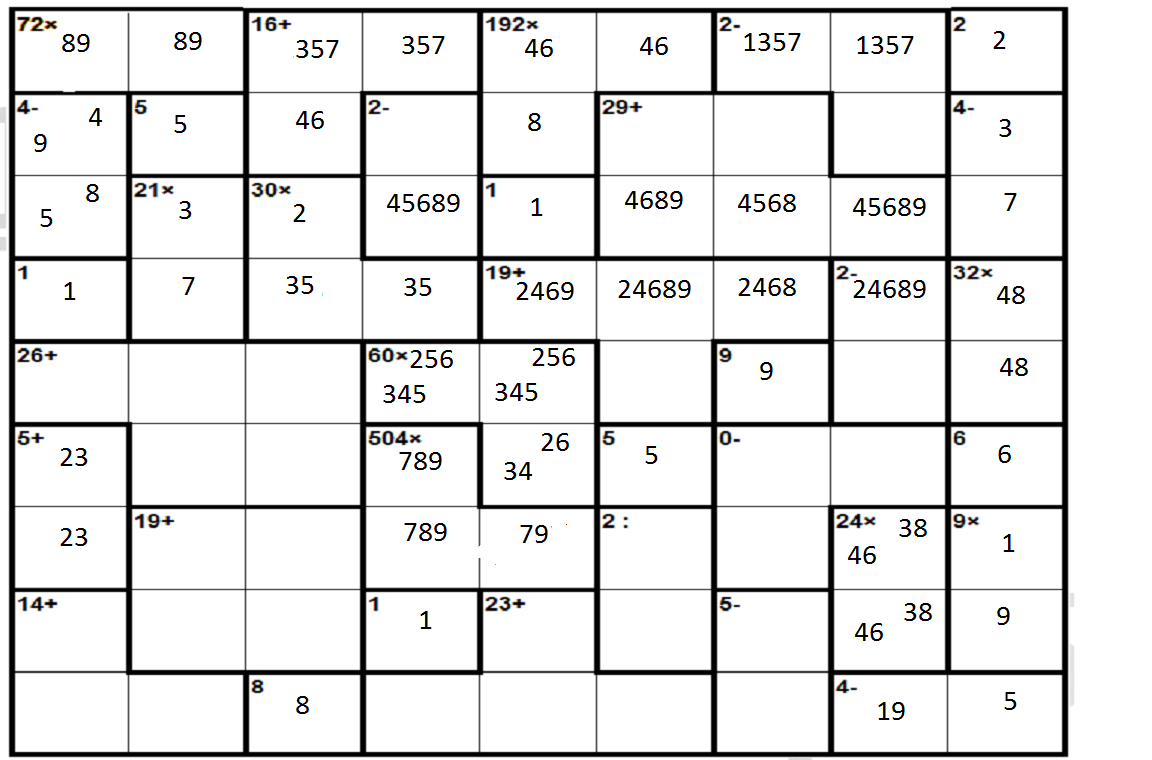 Uploaded with [url=http://www.calcudoku.org/im/forum/img_f3_t236_p2374_i2.png]ImageShack.us[/url] "4-"(a2)=[4,8],[5,9] From now on I used [4,8] and I developed the rest of the diagram by pure analysis till an impossible situation. Then I restarted from the same point using the hypothesis [5,9] until the final and correct solution. So the question : This must be considered a TAE solution or an analytical solution? What your opinion? ( This is the method I always use when I don't know how to continue analytically, particularly in the 9x9 ). _________________Visit http://www.calcudoku.org the most interesting and addictive site of puzzles.
|
|

|
 |
arjen 
Posted on: Sun Jun 10, 2012 9:42 am
Posts: 49
Joined: Sun Oct 16, 2011 10:58 am

|
 Re: More fuel to the fire Total of known numbers first 3 columns = 107
3*45 - 107 = 28 left for "-4" and c1, c2 & c4
Possible series for c1,c2,c4 by
[4,8] = [3,6,7] & [4,5,7]
[5,9] = [3,4,7] & [3,5,6]
[4,8] & [4,5,7] is invalid because of the 4 on a2 & c2
[5,9] & [3,4,7] is invalid because of the 5 on d1 & d4
that makes c2 = 6 -> [37] for c1 & d1 -> 2 for h2
|
|

|
 |
jomapil 
Posted on: Sun Jun 10, 2012 11:23 am
Posts: 246
Location: Lisbon, Portugal
Joined: Sun Sep 18, 2011 5:40 pm

|
 Re: More fuel to the fire Good point, Arjen.
The rule of the sum of columns ( or rows ) has many facets ( aspects ). I didn't see that. I must dedicate more attention and concentration to follow the ways smarter and more interesting of the analysis and not the ways simpler and more immediate of TAE but much more complicated, more laborious and more time-consuming.
But the question is still present : My resolution, ( although with a " little " TAE ), can be considered Analytical or TAE?
In other words, what is TAE method and Analytical method? What is the border between the two methods?
_________________Visit http://www.calcudoku.org the most interesting and addictive site of puzzles.
|
|

|
 |
mce 
Posted on: Sun Jun 10, 2012 3:44 pm
Posts: 13
Joined: Sun Mar 04, 2012 6:46 pm

|
 Re: More fuel to the fire Jomapil is right. There is no clear boundary between TAE and Fully Analytical Solution (hereby baptized "FAS" ![Smile [smile]](./images/smilies/msp_smile.gif) ). Even though I agree that taking random shots until everything fits is not "the correct approach", and that neither would brute forcing all possible solutions be "correct", I find the whole debate around "my solution approach is better then yours because you used TAE at some point while I have a FAS" quite silly. Many of the so called FAS that I've seen discussed in the forum include steps like "we see that a3 cannot be 4, because if it were then a6 would have to be 8, which is not possible because d6 already is known to be 8". I can call that TAE if I want: we try a 4 in a3 and discover that it's an error, even if we never write down the 4. In short, the whole TAE vs. FAS topic is badly defined and cannot be otherwise. A more relevant distinction between "good" and "bad", or with better terminology "elegant" and "less elegant" or "clumsy", would be based on how many solution steps are used, where every time one has to backtrack a cell is also counted as a "step". Just like in mathematics, where a proof is considered more elegant if it requires less steps, or required less "parallel" cases, and where an analytical proof is valued higher than an exhaustive computer proof that just explores all possible combinations. The trouble is that for these puzzles it still not possible to define such elegance in a measurable way. What one person does in his or her head, another does on paper, and a third one does online. Only the last case can be measured somewhat accurately (if it weren't for typos), but such measurement still is meaningless as long as the other approaches exist as a preparation.
|
|

|
 |
jaek 
Posted on: Sun Jun 10, 2012 4:17 pm
Posts: 300
Joined: Fri Jun 17, 2011 8:15 pm

|
 Re: More fuel to the fire I'm afraid this is all about your own definitions. I think that if I am juggling the numbers around in my head trying to follow them out to a conflict; find a conflict; then go back to follow a different path, that is still analytical. But as soon as I get 5 or 6 steps down a path; forget which number I'd put in a given cell; and go back to write it down/type it out/etc. then I've switched to TAE. And for the record I do that on a regular basis out of frustration, laziness, what have you. I know I have a dozen puzzles to do every day, so if I'm mired in a 6x6 and a guess will get me through it quicker then I'm not averse to that. Or in a larger puzzle when large portions are complete. I try to avoid it when I there are still any, many cells open because the chances of discovering a contradiction quickly are fewer.
In addition, I generally think that if I find myself going 5 or 6 steps down a particular path then I have probably missed something somewhere else. So even if I do get to a solution without what I would consider TAE, I still sometimes think there must have been an even more analytical solution.
|
|

|
 |
jomapil 
Posted on: Sun Jun 10, 2012 4:55 pm
Posts: 246
Location: Lisbon, Portugal
Joined: Sun Sep 18, 2011 5:40 pm

|
 Re: More fuel to the fire Mce and Jaek: Your opinions come to reinforce my thoughts - almost every puzzles have a component TAE and a component FAS. ( of course, the simplest 4x4, 5x5 and some 6x6 can be purely FAS ). But the most of the puzzles are a combination of those two.Even when Clm says all the puzzles can be solved by FAS, there will always be the component TAE. The praiseworthy objective is to reduce the more possible the TAE for all good reasons.
_________________Visit http://www.calcudoku.org the most interesting and addictive site of puzzles.
|
|

|
 |
clm 
Posted on: Sun Jun 10, 2012 9:40 pm
Posts: 856
Joined: Fri May 13, 2011 6:51 pm

|
 Re: More fuel to the fire jomapil wrote: Mce and Jaek: Your opinions come to reinforce my thoughts - almost every puzzles have a component TAE and a component FAS. ( of course, the simplest 4x4, 5x5 and some 6x6 can be purely FAS ). But the most of the puzzles are a combination of those two.Even when Clm says all the puzzles can be solved by FAS, there will always be the component TAE. The praiseworthy objective is to reduce the more possible the TAE for all good reasons. Hi, jomapil, first have a look to this “analysis”, which in fact does not essentially differ from the one detailed by arjen. 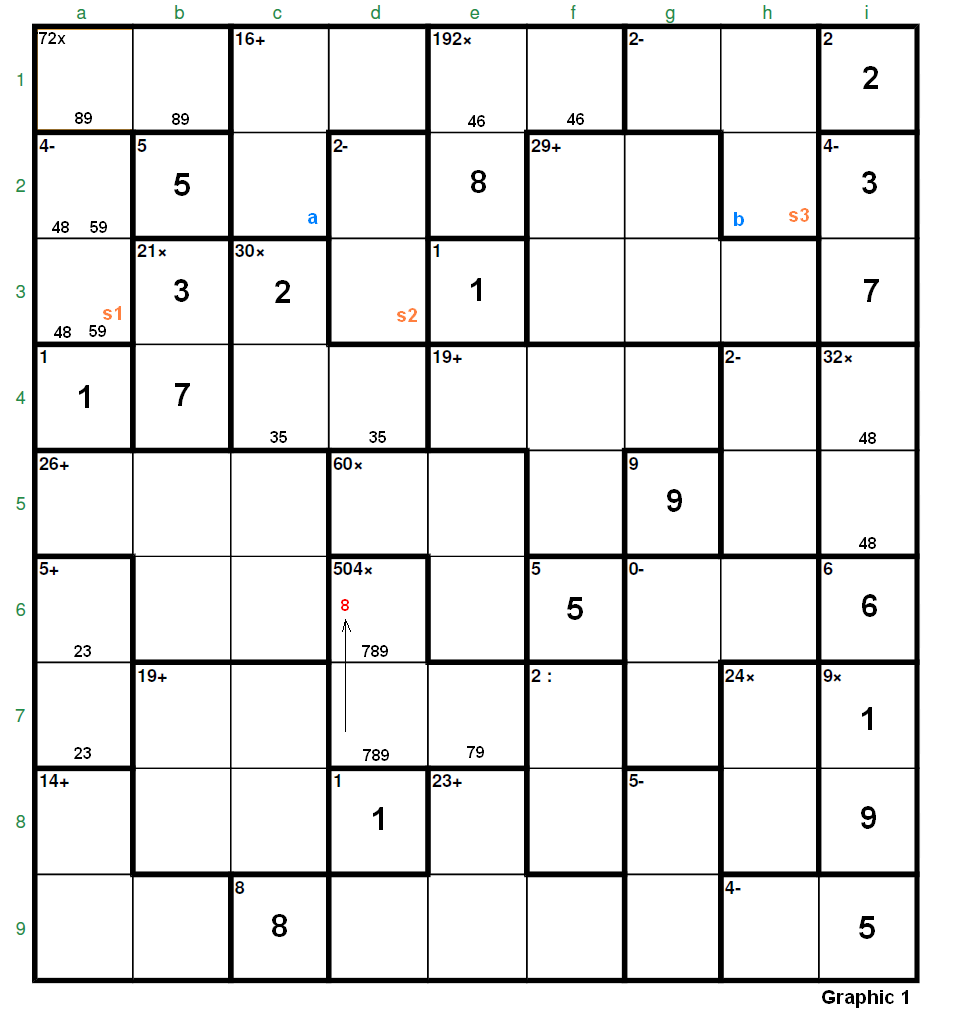 It is clear that c3 = 2 has been determined using the parity rule (analysis). Let’s name s1 the sum of numbers in cage “4-”, s2 the sum of numbers in cage “2-” (d2-d3) and s3 the sum of numbers in cage “2-” (g1-h1-h2). And also, for simplicity, let’s name “a” the value of the cell c2 and “b” the value of the cell h2. We have: s1 + s2 + s3 = 32 (addition rule to rows 1, 2 and 3). And also, considering the sum (45) of numbers in row 1, we have: 45 + a + b = 17 + 16 + 10 + s3 + 2 >>> a + b = s3, where g1 + h1 + b = s3 and then a = g1 + h1. Let’s proceed with these two equations: s2 could initially be [2,4] (6), [4,6] (10) or [5,7] (12). If s2 = 12 (d2 = 7, d3 = 5) >>> s1 = [4,8] = 12 then s3 = 8 >>> [1,2,5], then h2 = 2, g1-h1 = [1,5] and c2 = a = g1 + h1 = 1 + 5 = 6 (the arjen’s solution). Two cases for s2 = 10 = [4,6]: s1 = 12 ([4,8]) >>> s3 = 10 >>> [1,3,6] with b = 6 and this is invalid because a = g1 + h1 = 1 + 3 = 4, impossible, it goes against the hypothesis [4,6] for s2. s1 = 14 ([5,9]) >>> s3 = 8 = [1,2,5] (the previous arjen’s solution). And two cases for s2 = 6 (d2 = 2, d3 = 4): s1 = 12 >>> s3 = 14 which is impossible because it would require an 8 as the higher number inside the cage “2-” (g1-h1-h2) but the 8’s are forbidden in rows 1 and 2. s1 = 14 >>> s3 = 12 >>> [1,4,7] (the 2’s now unavailable in rows 1, 2 and 3) >>> h2 = 4 >>> g1-h1 = [1,7] >>> a = g1 + h1 = 1 + 7 = 8, which is impossible due to e2 = 8. Consequently, “2-” (g1-h1-h2) = [1,2,5] with h2 = 2 and g1-h1 = [1,5] >>> a = 1 + 5 = 6. Also (see Graphic 2), s1 cann’t be [4,8] because now s2 = 12 = [5,7] would produce two 3’s in d1 and d4. So “4-” = [5,9] >>> a2 = 9, a3 = 5, and s2 = 10 = [4,6] >>> d2 = 4 and d3 = 6.  With respect to our old and “Byzantine” discussion on TAE and FAS, I think that some people find very useful the TAE most time then OK, but I prefer to do some previous calculations, let’s initially admit that these fall in the field of the “analysis” ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) , in my opinion they may reduce the time for the solution, though bored at the beginning. Unfortunately (or not?) the calcudoku is not an exact science, we do not have theorems yet ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) , as in mathematics, of course. Actually nobody would try to find the roots of x^2 - 5x + 4 = 0, that is [1,4], by TAE, though it’s possible and very easy, because we have the formula that gives us directly the roots, but certainly the roots of x^2 - 2x - 4 = 0 (1 plus the square root of 5 and 1 minus the square root of 5) by TAE would require “infinite” time ![Mad [mad]](./images/smilies/msp_mad.gif) , being the square root of 5 an irrational number (well, the engineers feel comfortable with a few decimals ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) ). Anyway we are free to name every process (even the main rules) TAE if we like. My opinion on your initial question is that what you have made is a TAE (“a little TAE”, as you say, considering we have only 2 options for the cage “4-”), I think that before that we had other possibilities, as in the arjen’s proposal, for instance. Let's provide the solution ("for the future"): 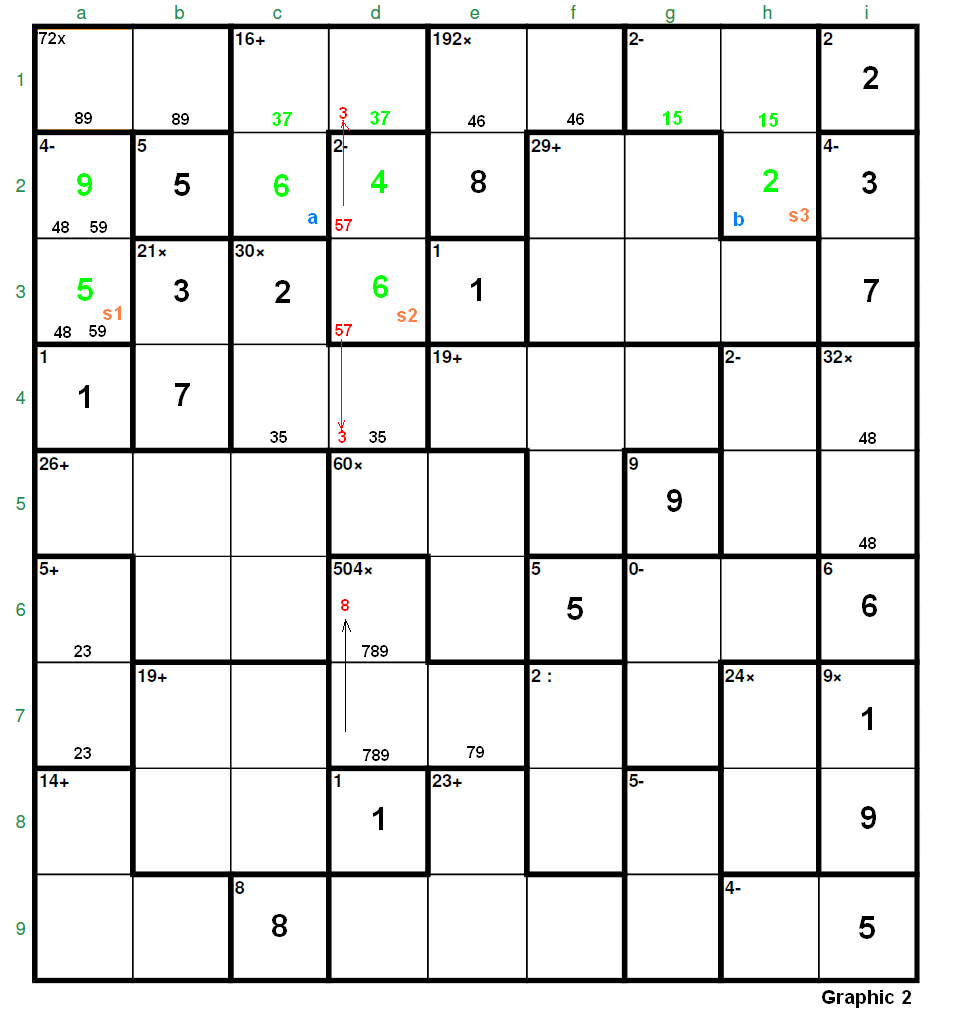
|
|

|
 |
jotempe 
Posted on: Mon Jun 11, 2012 9:59 am
Posts: 31
Joined: Mon Mar 05, 2012 12:45 pm

|
 Re: More fuel to the fire jaek wrote: I'm afraid this is all about your own definitions. I think that if I am juggling the numbers around in my head trying to follow them out to a conflict; find a conflict; then go back to follow a different path, that is still analytical. But as soon as I get 5 or 6 steps down a path; forget which number I'd put in a given cell; and go back to write it down/type it out/etc. then I've switched to TAE. And for the record I do that on a regular basis out of frustration, laziness, what have you. I know I have a dozen puzzles to do every day, so if I'm mired in a 6x6 and a guess will get me through it quicker then I'm not averse to that. Or in a larger puzzle when large portions are complete. I try to avoid it when I there are still any, many cells open because the chances of discovering a contradiction quickly are fewer.
That's exactly what I said before. The classificaton of a soluton (analytical vs. TAE) depends on the 'mental agility' of the solver, on how many steps of a hypothesis he can go before he needs to start puttng the numbers down on diagram. There exist, of course, diagrams that can be solved in a completely straightforward way, without need for ad absurdum kind of reasoning, that is building hypotheses, and showing that they lead to a contradiction. But the majority do require some of that, and people may have dfferent views on the question if the solution is analytical. I, for one, find that wth Patrck's diagrams I most often need to do TAE on 6x6 patterned and 8x8 difficult. I is long time since I last needed TAE on a 12x12 diagram (and that was most probably because at that tme I didn't know all the tricks, that I know now ![Drool [drool]](./images/smilies/msp_drool.gif) ). I now solve all 12x12 in memory, only occasionally using a calculator to factor a large product, or a piece of paper to note possible combinations in a larger cage. Also almost all 10x10 dagrams here can be solved in memory. Many 8x8, on the other hand, requre TAE, and often wth multiple "branching points", that is neither assumption about the content of some cell leads straight to a contradiction, and you have to make another guess before you know which one is correct.
|
|

|
 |
jomapil 
Posted on: Mon Jun 11, 2012 10:56 am
Posts: 246
Location: Lisbon, Portugal
Joined: Sun Sep 18, 2011 5:40 pm

|
 Re: More fuel to the fire Jotempe I'm completely with you! I use exclusively FAS with 10x10 and 12x12. Some of 6x6 difficult I use TAE. But you forgot one type, the 9x9's that I use TAE and FAS particularly the patterned 9x9 of the Tuesdays. ( The 9x9 of today I used exclusively Analytical method ).
_________________Visit http://www.calcudoku.org the most interesting and addictive site of puzzles.
|
|

|
 |
clm 
Posted on: Mon Jun 11, 2012 1:07 pm
Posts: 856
Joined: Fri May 13, 2011 6:51 pm

|
 Re: More fuel to the fire jomapil wrote: Jotempe I'm completely with you! I use exclusively FAS with 10x10 and 12x12. Some of 6x6 difficult I use TAE. But you forgot one type, the 9x9's that I use TAE and FAS particularly the patterned 9x9 of the Tuesdays. ( The 9x9 of today I used exclusively Analytical method ). Hi, jomapil, congrats!, you are obtaining more and more solutions with analytical methods ![ThumpUp [thumbup]](./images/smilies/msp_thumbup.gif) . Btw, I would like to add something (now that we are more familiarized with the philosophy for the initial phase of that Jun 06, 2012, 9x9 puzzle) to my yesterday's "analysis". It can be useful to you (and perhaps to more calcudokers). It is the possibility of applying “The use of maximums and minimums in the sum of cages” (there is a topic on this subject, Jun 21, 2011, in this same section “Solving strategies and tips”). It’s a powerful tool that I use some times, though in our actual discussion does not look specially relevant, but we can practice a little bit with it. The idea is the following: Instead of commencing the “analysis” with the cage “2-” (d2-d3) we will determine the unique combination for the cage “2-” (g1-h1-h2). Considering the same first equation: s1 + s2 + s3 = 32, we define the boundaries for s3 (let’s remind, anyway, that the higher number, the number from which the other are subtracted, in a cage “n-”, which sum is “s”, regardless of the number of cells, is always equal to (s + n) / 2)). Since the maximum values of s1 and s2 (among the possibilities) are 14 and 12 (which sum is 26), the minimum value for s3 will be 6. And since the minimum values of s1 and s2 (among the possibilities) are 12 and 6 (which sum is 18), the maximum value for s3 will be 14. So, being s3 an even cage, it must be 6, or 8, or 10, or 12, or 14. At a first glance, the value 16 for s3, that is, when a 9 is inside, does not “exist”, in the other hand that’s very easy to deduce. Now let’s go with those 5 values: s3 = 6 >>> [1,1,4], cancelled; s3 = 14 = [x,y,8], cancelled; s3 = 12 = [1,4,7] >>> h2 = 4 >>> c2 = 1 + 7 (from the yesterdays’s second equation) = 8, cancelled; s3 = 12 = [2,3,7] >>> h2 = 2 >>> c2 = 3 + 7 = 10, cancelled. Finally, s3 = 10 >>> [2,2,6], cancelled, or [1,3,6] >>> h2 = 6 >>> c2 = 1 + 3 = 4. But now s1 + s2 = 22. If s1 = 14 ([5,9]) then s2 = 8 = [3,5], cancelled; and if s1 = 12 ([4,8]) then s2 = 10 = [4,6], cancelled (due to the conflict with the hypothesis, in other words, the presence of both, the 4 and the 6, in row 2). So we are left again with the only possibility s3 = 8 = [1,2,5] >>> h2 = 2, g1-h1 = [1,5] and c2 = 1 + 5 = 6 and from this point we join the original line of reasoning exposed yesterday.
|
|

|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
|

|

![Smile [smile]](./images/smilies/msp_smile.gif) ). Even though I agree that taking random shots until everything fits is not "the correct approach", and that neither would brute forcing all possible solutions be "correct", I find the whole debate around "my solution approach is better then yours because you used TAE at some point while I have a FAS" quite silly. Many of the so called FAS that I've seen discussed in the forum include steps like "we see that a3 cannot be 4, because if it were then a6 would have to be 8, which is not possible because d6 already is known to be 8". I can call that TAE if I want: we try a 4 in a3 and discover that it's an error, even if we never write down the 4. In short, the whole TAE vs. FAS topic is badly defined and cannot be otherwise.
). Even though I agree that taking random shots until everything fits is not "the correct approach", and that neither would brute forcing all possible solutions be "correct", I find the whole debate around "my solution approach is better then yours because you used TAE at some point while I have a FAS" quite silly. Many of the so called FAS that I've seen discussed in the forum include steps like "we see that a3 cannot be 4, because if it were then a6 would have to be 8, which is not possible because d6 already is known to be 8". I can call that TAE if I want: we try a 4 in a3 and discover that it's an error, even if we never write down the 4. In short, the whole TAE vs. FAS topic is badly defined and cannot be otherwise.
![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif)
![Mad [mad]](./images/smilies/msp_mad.gif) , being the square root of 5 an irrational number (well, the engineers feel comfortable with a few decimals
, being the square root of 5 an irrational number (well, the engineers feel comfortable with a few decimals 
![Drool [drool]](./images/smilies/msp_drool.gif) ). I now solve all 12x12 in memory, only occasionally using a calculator to factor a large product, or a piece of paper to note possible combinations in a larger cage. Also almost all 10x10 dagrams here can be solved in memory. Many 8x8, on the other hand, requre TAE, and often wth multiple "branching points", that is neither assumption about the content of some cell leads straight to a contradiction, and you have to make another guess before you know which one is correct.
). I now solve all 12x12 in memory, only occasionally using a calculator to factor a large product, or a piece of paper to note possible combinations in a larger cage. Also almost all 10x10 dagrams here can be solved in memory. Many 8x8, on the other hand, requre TAE, and often wth multiple "branching points", that is neither assumption about the content of some cell leads straight to a contradiction, and you have to make another guess before you know which one is correct.![ThumpUp [thumbup]](./images/smilies/msp_thumbup.gif) .
.