The "rule of quadrants" - 6x6 difficult from 09-May-2012
| Author |
Message |
jotempe 
Posted on: Thu May 10, 2012 8:18 am
Posts: 31
Joined: Mon Mar 05, 2012 12:45 pm

|
 The "rule of quadrants" - 6x6 difficult from 09-May-2012 Maybe this rule is known, but I have never seen it mentioned in the strategy posts... So here it goes: Quote: For even-sized puzzles (4x4, 6x6, 8x8...): if you divide the puzzle in for equal quadrants along its horizontal and vertical symmetry axes, then the top left quadrant contains the same numbers as the bottom right one. Analogically the top right quadrant has same numbers as bottom left It is really easy to prove it. See how this works on yesterday's 6x6 pattern puzzle:  1. Notice, that 18x cage can be only with (1,3,6). So, the vertical 18x tells you, that the 13+ cage contains 2 and 5 in this column. Thus, the third number in the 13+ cage must be 6. 2. Now look at the vertical 30x cage. It could be either (2,3,5) or (1,5,6). However we already know, that it can not contain 6, so it is (2,3,5) and therefore the cell in the third row contains 1. 3. Same holds for the horizontal 30x cage. It must be (2,3,5), because it can not contain 1 - so the second number in the 0- cage is 6. Therefore the last missing number in this cage must be 5, and we cal fill the entire top left quadrant: 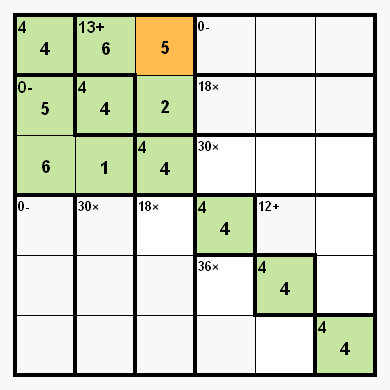 4. Now enter the rule above: the bottom right quadrant must contain the same numbers, so we have 1,2,5,5,6,6 to put into it, to make 36x and 12+ cages. There is only one way to do it: (1,6,6), and (2,5,5) - thus we can fill this quadrant immediately:  5. The rest is now trivial, we just fill the remaining numbers into their only possible places: first 5s and 6s, then 1s and 2s, then 3s. Puzzle solved 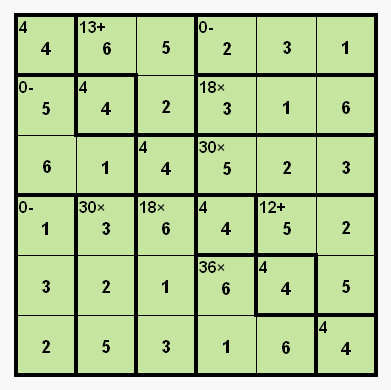 The rule becomes less useful with larger diagrams, but still it can sometimes help with them.
|
|

|
 |
clm 
Posted on: Thu May 10, 2012 10:51 am
Posts: 856
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The "rule of quadrants" - 6x6 difficult from 09-May-2012 jotempe wrote: Maybe this rule is known, but I have never seen it mentioned in the strategy posts... So here it goes: Quote: For even-sized puzzles (4x4, 6x6, 8x8...): if you divide the puzzle in for equal quadrants along its horizontal and vertical symmetry axes, then the top left quadrant contains the same numbers as the bottom right one. Analogically the top right quadrant has same numbers as bottom left It is really easy to prove it. ..... This subject has been fully exposed in the thread "Something I've always been curious about" in this same section "Solving strategies and tips" including the demonstration for the equal numbers in the quadrants in the case of that type of 6x6 (i.e., the Nov 21, 2011 post); additional and interesting discussion on the structutre of the bottom right quadrant is extensively held there. The same reasoning and philosophy can be logically applied to wider even-sized puzzles but that division into quadrants has never appeared in the 8x8's (nor in the 10x10's, ... ); in the case of the 4x4's the topic "Why in a 4x4 numbers in corners are those in inner area" (same section) shows that equality between corners and inner area ... , in the particular case of a division into 4 2x2 quadrants in a 4x4 the quadrants certainly should contain the same numbers but the 4x4's in general are very fast to solve.
|
|

|
 |
pnm 
Posted on: Thu May 10, 2012 11:01 am
Posts: 3301
Joined: Thu May 12, 2011 11:58 pm

|
 Re: The "rule of quadrants" - 6x6 difficult from 09-May-2012 clm wrote: This subject has been fully exposed in the thread "Something I've always been curious about" in this same section "Solving strategies and tips" including the demonstration for the equal numbers in the quadrants in the case of that type of 6x6 (i.e., the Nov 21, 2011 post); additional and interesting discussion on the structutre of the bottom right quadrant is extensively held there. On another note, clm, it's time for you to write your "Definitive Guide to Solving Calcudoku Puzzles" and publish it  (seriously!) Patrick
|
|

|
 |
jomapil 
Posted on: Thu May 10, 2012 11:41 am
Posts: 246
Location: Lisbon, Portugal
Joined: Sun Sep 18, 2011 5:40 pm

|
 Re: The "rule of quadrants" - 6x6 difficult from 09-May-2012 But, Jotempe, this rule is only for this diagram? Or is it universal?
And the diagram must be divided in four quadrants? I verified several puzzles and it looks like that it applies for ALL the diagrams. Is it so?
_________________Visit http://www.calcudoku.org the most interesting and addictive site of puzzles.
|
|

|
 |
jotempe 
Posted on: Thu May 10, 2012 1:17 pm
Posts: 31
Joined: Mon Mar 05, 2012 12:45 pm

|
 Re: The "rule of quadrants" - 6x6 difficult from 09-May-2012 Yes, it is universal for all even-sized puzzles. There is a "sort of" generalisation, but I don't know if it would be useful for solving real puzzles: If you divide any diagram (not necesairly even-sized) into four parts, by one horizontal and one verical line (again, not necesairly symetrically), in such a way, to get two sqares and two rectangles then those rectangular parts would have the same numbers in them.
|
|

|
 |
clm 
Posted on: Thu May 10, 2012 2:24 pm
Posts: 856
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The "rule of quadrants" - 6x6 difficult from 09-May-2012 pnm wrote: clm wrote: This subject has been fully exposed in the thread "Something I've always been curious about" in this same section "Solving strategies and tips" including the demonstration for the equal numbers in the quadrants in the case of that type of 6x6 (i.e., the Nov 21, 2011 post); additional and interesting discussion on the structutre of the bottom right quadrant is extensively held there. On another note, clm, it's time for you to write your "Definitive Guide to Solving Calcudoku Puzzles" and publish it  (seriously!) Patrick But this is just a hobby (very nice indeed), prepearing a book would take me 1 or 2 years of work ... ![Scared [scared]](./images/smilies/msp_scared.gif) ; in the other hand, even in this specialized site perhaps only 25 to 30 puzzlers (among 3200) look to be really interested in these subjects, think in the very few solutions, 8 if I remember well, sent to the "Christmas puzzle", less for the "Nicow's Red Cross" puzzles, or even your last 9x9 with a solver rating of 140 that you provided on May 07 in "Any suggestions?" (no feedbacks until the moment) ... . A different thing is the number of visits to some specific rules or questions, this in my opinion is more related to the "day by day" activity (for instance, for the topic "Full tables ... " I have observed that the visits are more concentrated those days when the "bitwise OR" or the "mod function" appear, etc.). But, seriously, from a business point of view, what do you think about putting in the market some kind of simple toy (in plastic, with the cooperation of Geyper, Lego, ... ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) ) with different sets of pieces (cage shapes, ... , for various different levels with different sets of calcudokus), don't you think it would be better than the scrabbles, masterminds, scatergoris, monopolys, etc.?.
|
|

|
 |
clm 
Posted on: Thu May 10, 2012 2:35 pm
Posts: 856
Joined: Fri May 13, 2011 6:51 pm

|
 Re: The "rule of quadrants" - 6x6 difficult from 09-May-2012 jotempe wrote: Yes, it is universal for all even-sized puzzles. There is a "sort of" generalisation, but I don't know if it would be useful for solving real puzzles: If you divide any diagram (not necesairly even-sized) into four parts, by one horizontal and one verical line (again, not necesairly symetrically), in such a way, to get two sqares and two rectangles then those rectangular parts would have the same numbers in them. Absolutely true, the affirmation is universal and the demonstration is very easy since if you have any number "n", lets's say the 5, "t" times in the rectangle, considering, for instance, the rows, you need the number 5 another (r - t) times (being r the number of rows of the rectangle) in the "complementary" square and thus again r - (r - t) = t times in the opposite rectangle, so the same number of times for every number being considered (if the side of the square is r the "opposite" rectangle covers r columns as well), that is, for all numbers in the rectangle. The applicability of this property is another question because, as commented, i.e., in puzzles larger than 6x6 I cann't remember any case where that division by two axis has been possible (in the case of 7x7's, 8x8's, 10x10's, 12x12's, ... , though it happens some times in the 9x9's, in the relatively frequent structure, usually on tuesdays, like the one proposed by Patrick in "Any suggestions?" on May 07, in which case the 4x5 rectangles have 20 numbers, big rectangles or big set of numbers, and the rule, though mathematically true, is not practical). As an example try to apply it in this case to see the difficulties.
|
|

|
 |
jomapil 
Posted on: Thu May 10, 2012 5:57 pm
Posts: 246
Location: Lisbon, Portugal
Joined: Sun Sep 18, 2011 5:40 pm

|
 Re: The "rule of quadrants" - 6x6 difficult from 09-May-2012 The "demonstration" of Clm or better his logical reasoning is a perfect justification for the "rule".
But his observation for the greater than 6x6... even so I think it can be useful ( although in some cases can be of difficult use ) due also the applicability at two squares and two rectangles.
_________________Visit http://www.calcudoku.org the most interesting and addictive site of puzzles.
|
|

|
 |
picklepep 
Posted on: Fri May 11, 2012 4:25 am
Posts: 98
Joined: Fri May 13, 2011 12:48 am

|
 Re: The "rule of quadrants" - 6x6 difficult from 09-May-2012 jomapil wrote: The "demonstration" of Clm or better his logical reasoning is a perfect justification for the "rule".
But his observation for the greater than 6x6... even so I think it can be useful ( although in some cases can be of difficult use ) due also the applicability at two squares and two rectangles. I like your discussions - clm - because often times it will lead me to think about the puzzles slightly different. This happened when you were discussing the 7x7 only - op and brought up the fact that often times the 'odd' square can very easily be found to be even or odd. I have since applied this method in various other puzzles to eliminate half the possibilities! A very useful tool. While i usually solve the 6x6 pattern with other methods, I never really thought about how filling in a block of numbers neccitates that their be an isomorph opposite it. I believe that this can be a very powerful tool! Thank you for putting so much time into your analysis!
|
|

|
 |
jomapil 
Posted on: Fri May 11, 2012 10:46 am
Posts: 246
Location: Lisbon, Portugal
Joined: Sun Sep 18, 2011 5:40 pm

|
 Re: The "rule of quadrants" - 6x6 difficult from 09-May-2012 jomapil wrote: The "demonstration" of Clm or better his logical reasoning is a perfect justification for the "rule".
But his observation for the greater than 6x6... even so I think it can be useful ( although in some cases can be of difficult use ) due also the applicability at two squares and two rectangles. Clm, you are right as always: In fact for greater than 6x6 it is very hard to profit this rule. _________________Visit http://www.calcudoku.org the most interesting and addictive site of puzzles.
|
|

|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
|

|





![Scared [scared]](./images/smilies/msp_scared.gif) ; in the other hand, even in this specialized site perhaps only 25 to 30 puzzlers (among 3200) look to be really interested in these subjects, think in the very few solutions, 8 if I remember well, sent to the "Christmas puzzle", less for the "Nicow's Red Cross" puzzles, or even your last 9x9 with a solver rating of 140 that you provided on May 07 in "Any suggestions?" (no feedbacks until the moment) ... . A different thing is the number of visits to some specific rules or questions, this in my opinion is more related to the "day by day" activity (for instance, for the topic "Full tables ... " I have observed that the visits are more concentrated those days when the "bitwise OR" or the "mod function" appear, etc.).
; in the other hand, even in this specialized site perhaps only 25 to 30 puzzlers (among 3200) look to be really interested in these subjects, think in the very few solutions, 8 if I remember well, sent to the "Christmas puzzle", less for the "Nicow's Red Cross" puzzles, or even your last 9x9 with a solver rating of 140 that you provided on May 07 in "Any suggestions?" (no feedbacks until the moment) ... . A different thing is the number of visits to some specific rules or questions, this in my opinion is more related to the "day by day" activity (for instance, for the topic "Full tables ... " I have observed that the visits are more concentrated those days when the "bitwise OR" or the "mod function" appear, etc.).![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) ) with different sets of pieces (cage shapes, ... , for various different levels with different sets of calcudokus), don't you think it would be better than the scrabbles, masterminds, scatergoris, monopolys, etc.?.
) with different sets of pieces (cage shapes, ... , for various different levels with different sets of calcudokus), don't you think it would be better than the scrabbles, masterminds, scatergoris, monopolys, etc.?.