| View unanswered posts | View active topics |
It is currently Tue Apr 23, 2024 11:38 am ← Back to the Calcudoku puzzle page |
|
All times are UTC + 1 hour [ DST ] |
|
|
Page 1 of 2 |
[ 17 posts ] | Go to page 1, 2 Next |
| Print view | Previous topic | Next topic |
My new puzzles
| Author | Message |
|---|---|
|
Posted on: Thu Nov 15, 2012 6:44 am Posts: 54 Joined: Thu Nov 03, 2011 8:52 am |
When I realised that I was waiting for Tuesdays to solve the "pattern" CalcuDokus, I decided it was time to try to make my own. You might remember that I published time ago a book of Double CalcuDokus and one of Samurai Calcudokus. You might also rmember that I developed a web page with daily CalcuDokus. The controls to solve them online were not the most efficient and somebody (sorry, don't remember who) that my puzzles were of average difficulty.
Anyhow, I thought I had most of what I needed to develop pattern CalcuDokus, and so I started working on them. To modify the program I had was easy enough (I only develop 9x9 puzzles), but it turned out that to find the right patterns was not! We two of the patterns I tried out, my program didn't converge at all. It tried for hours, but it didn't makaneg to generate a single puzzle. In case you are curious, here they are:   These patterns consists of "islands" of cages that form separate "sub-puzzles". Especially the first one. That's why no unique solution could be found (I believe). It makes sense that a unique solution is only possible if there are enough crossings. Some patterns, like the two following ones, converge quickly to puzzles with unique solutions:   Then, with some patterns, my program requires many minutes to produce a puzzle. Here is an example of such a pattern:  I also found that the pattern CalcuDokus tend to be more difficult than the "unorderly" ones. Anyhow, I started working on a book of pattern CalcuDokus. But I wanted to be sure that all puzzles could be solved analytically. Unfortunately, the only way I have found to identify analytically solvable puzzles is to actually solve them. I know, if I cannot solve them, they can still be solvable... For example, I fail to solve perhaps half of Patrick's Tuesday puzzles. And yet, I don't think I am a bad solver, although definitely not a fast one. In any case, to write my book, I started generating pattern puzzles and solve them. Sometimes I made mistakes and had to start from scratch. Some other times, I got stuck and had to give up after struggling for hours. Here is an example of a puzzle that IMO requires guessing. Tell me whether you can solve it analytically. I cannot:  After days of solving puzzles, I realised that I was getting saturated. That's why I decided to write a book with 60 random puzzles and 40 pattern puzzles (because I am confident that the random ones are analytically solvable without actually having to solve them all). I had to stop. The book is availbale from Lulu in print (http://www.lulu.com/product/paperback/200-challenging-calcudokus/20484581) for 10 Australian Dollars or from Smashword (http://www.smashwords.com/books/view/255167) in several digital formats for US$1.99. Sooner or later, it will also be available from Amazon, Barnes & Noble, etc. Ciao, Giulio. |
|
|
|
|
Posted on: Thu Nov 15, 2012 10:28 am Posts: 3304 Joined: Thu May 12, 2011 11:58 pm |
hi Giulio,
thanks for the post/advert  yes: typically, the more "regular" the patterned arrangement, the more likely it is the puzzle will have permutations (of the numbers) that are also valid solutions. You need to have "interlocked dependencies" (what to call them) to get puzzles with a single solution. Good luck with the book. I would change the description though: now, on the Lulu page it says "CalcuDokus, introduced in 2004 as KenKen® (a registered trademark of Nextoy LLC), is a 9x9 numeric puzzle similar to Sudoku. But, unlike Sudoku, CalcuDoku doesn't require you to learn complex strategies." There is no need to mention "kenken" and the trademark bit. Also, the puzzle was originally called "Kashikoku Naru" (but maybe you meant "introduced in the US"). And, as you know, Calcudoku is not always a 9x9 puzzle. Next we can discuss "doesn't require you to learn complex strategies" ??? "Unlike Sudoku" ?? Finally, I prefer "Calcudoku" over "CalcuDoku", but that's just my personal preference  Patrick |
|
|
|
|
Posted on: Thu Nov 15, 2012 12:53 pm Posts: 54 Joined: Thu Nov 03, 2011 8:52 am |
Hi Patrick,
Thanks for the good wishes, although, I have to admit, I have given up to making any reasonable/substantial/significant/non-negligible (take your pick) amount of money with these books of puzzles! Quote: There is no need to mention "kenken" and the trademark bit. Yes, but why not? If people search for KenKen and I don't mention it, they might not find me. Quote: Also, the puzzle was originally called "Kashikoku Naru" (but maybe you meant "introduced in the US"). I don't doubt that you are right, but I suspect that most people are as ignorant as I am! ![Drool [drool]](./images/smilies/msp_drool.gif) Quote: And, as you know, Calcudoku is not always a 9x9 puzzle. Of course, but: if people know it, they will notice that I only speak of 1-to-9 numbers and will understand that the book only includes 9x9s; if people don't know it, as I only generate 9x9, why should I care to tell them? ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) Quote: Next we can discuss "doesn't require you to learn complex strategies" ??? "Unlike Sudoku" ?? Well, I started solving CalcuDokus after solving lots of Sudokus, learning all possible strategies, and writing about them. Most of Sudoku's strategies rely on the fact that unicity is enforced on rows, columns, and boxes. In CalcuDoku there are no boxes. This at once eliminates complex Sudoku strategies like Swordfish. I find that with CalcuDokus you need to think logically, but the strategies are simpler. Quote: Finally, I prefer "Calcudoku" over "CalcuDoku", but that's just my personal preference I like words with capitals in the middle! Please,feel free to keep writing Calcudoku, I won't hold it against you! ![Wink [wink]](./images/smilies/msp_wink.gif) |
|
|
|
|
Posted on: Wed Nov 21, 2012 12:13 am Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
giulio wrote: When I realised that I was waiting for Tuesdays to solve the "pattern" CalcuDokus, I decided it was time to try to make my own. You might remember that I published time ago a book of Double CalcuDokus and one of Samurai Calcudokus. You might also rmember that I developed a web page with daily CalcuDokus. The controls to solve them online were not the most efficient and somebody (sorry, don't remember who) that my puzzles were of average difficulty. Anyhow, I thought I had most of what I needed to develop pattern CalcuDokus, and so I started working on them. To modify the program I had was easy enough (I only develop 9x9 puzzles), but it turned out that to find the right patterns was not! We two of the patterns I tried out, my program didn't converge at all. It tried for hours, but it didn't makaneg to generate a single puzzle. In case you are curious, here they are: ... These patterns consists of "islands" of cages that form separate "sub-puzzles". Especially the first one. That's why no unique solution could be found (I believe). It makes sense that a unique solution is only possible if there are enough crossings. Some patterns, like the two following ones, converge quickly to puzzles with unique solutions: ... Then, with some patterns, my program requires many minutes to produce a puzzle. Here is an example of such a pattern: ... I also found that the pattern CalcuDokus tend to be more difficult than the "unorderly" ones. Anyhow, I started working on a book of pattern CalcuDokus. But I wanted to be sure that all puzzles could be solved analytically. Unfortunately, the only way I have found to identify analytically solvable puzzles is to actually solve them. I know, if I cannot solve them, they can still be solvable... For example, I fail to solve perhaps half of Patrick's Tuesday puzzles. And yet, I don't think I am a bad solver, although definitely not a fast one. In any case, to write my book, I started generating pattern puzzles and solve them. Sometimes I made mistakes and had to start from scratch. Some other times, I got stuck and had to give up after struggling for hours. Here is an example of a puzzle that IMO requires guessing. Tell me whether you can solve it analytically. I cannot: 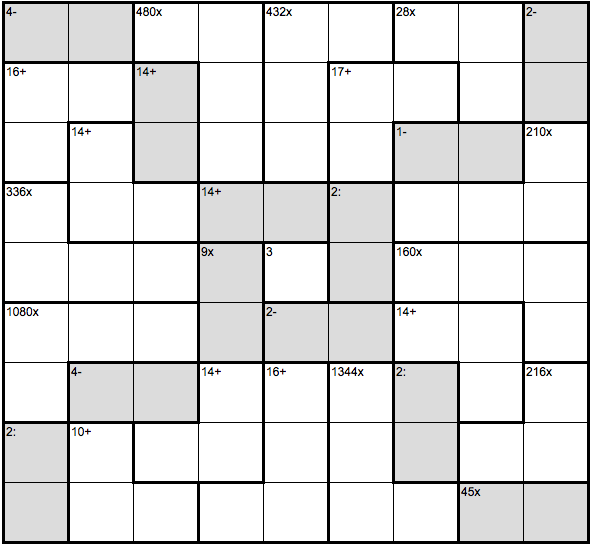 After days of solving puzzles, I realised that I was getting saturated. That's why I decided to write a book with 60 random puzzles and 40 pattern puzzles (because I am confident that the random ones are analytically solvable without actually having to solve them all). I had to stop. The book is availbale from Lulu in print (http://www.lulu.com/product/paperback/200-challenging-calcudokus/20484581) for 10 Australian Dollars or from Smashword (http://www.smashwords.com/books/view/255167) in several digital formats for US$1.99. Sooner or later, it will also be available from Amazon, Barnes & Noble, etc. Ciao, Giulio. The new patterns are always interesting and generally challenging since they come with new concepts. In the particular puzzle you propose this time, certainly very difficult (BTW, Patrick, I am very curious about your “difficulty level” of this Giulio’s puzzle, if you were so kind … if you need the translation into the code I can prepare that part and send it), I think the difficulty comes from the fact of having only one “single cell cage”, the 3 in the center of the grid (e5). In my opinion the only way to solve it is by exhaustive and hard analysis, because only with trial and error (TAE) it would be practically impossible due to the many combinations among the cages. Possibly the pattern with 5 given cells (five 1-cell cages) is “easier” than the proposed and the patterns with 9 given cells (nine 1-cell cages) even more “easier”. The pattern with all 3-cell cages (27 cages) could be very curious and interesting (and difficult to obtain as you comment because the unicity of the solutions must be guaranteed). Since a few days have already elapsed and no comments have been sent yet I assume you do not mind if I provide part (2 rows) of my solution (solution unique in my opinion) just to verify that it’s the same you have. In about a week (perhaps more calcudokers are still interested in this puzzle) we could send the full solution: 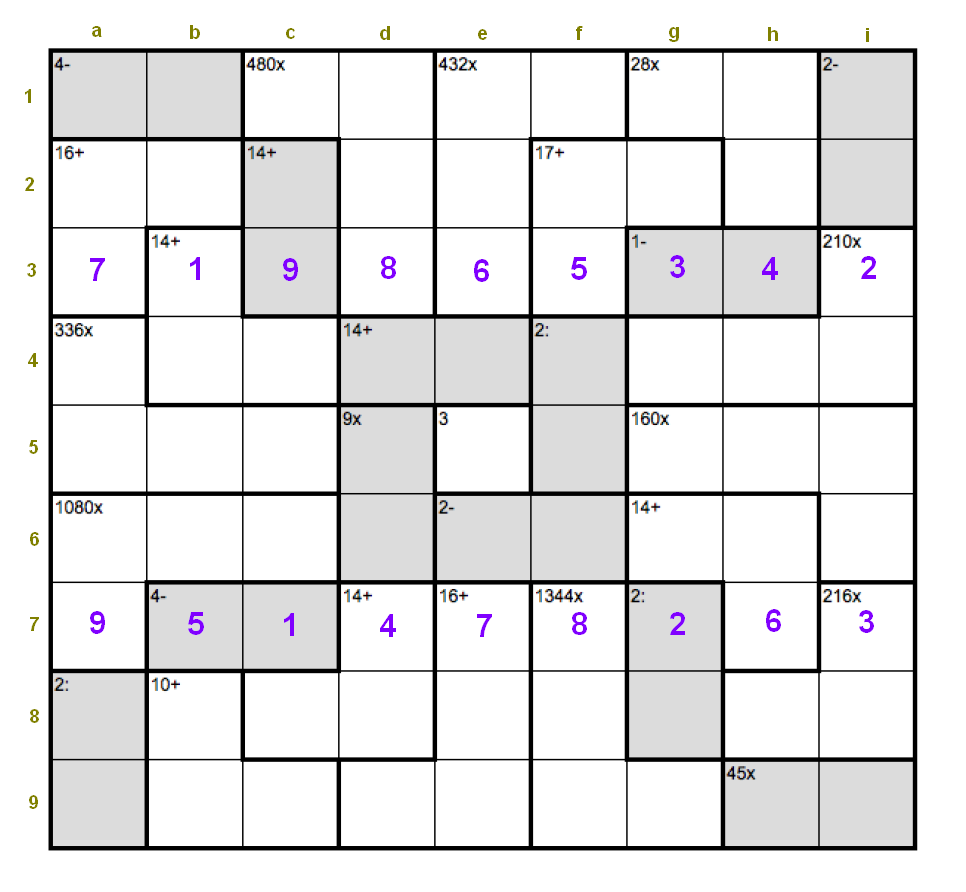 |
|
|
|
|
Posted on: Wed Nov 21, 2012 1:38 am Posts: 54 Joined: Thu Nov 03, 2011 8:52 am |
Hi clm,
Congratulations! The two rows you provided match those of the solution I have. This is the solution given by my program, because I was not able to solve the puzzle myself without guessing, although, the distinction between "exhaustive and hard analysis" and trial and error is sometimes difficult to make. I always solve the puzzles with pencil, after printing them. I am fine as long as I can use the margins for analysis and write in the cells the combinations, but if the decision tree becomes very large, like in this puzzle, and I am unable to keep track of all the possibilities on the single page of the puzzle, I arrive to the conclusion that the puzzle cannot be solved analytically and give up (because I don't want to guess). I tried to solve this puzzle twice and got stuck both times... With the program that generates "random" puzzles (i.e., without patterns), I can set the maximum number of single-cell cages. Although I normally set it to 3, the resulting puzzles are not too difficult. It is not unusual the the generated puzzle only has one single-cell cage. I really think that the difficulty of the pattern CalcuDokus is due to the fact that there is a pattern. |
|
|
|
|
Posted on: Wed Nov 21, 2012 3:56 am Posts: 54 Joined: Thu Nov 03, 2011 8:52 am |
As today calcudocu.org dindn't publish a 9x9, I generated a puzzle with the same pattern clm commented on. I wanted to see whether it would also be too difficult [for me] to solve analytically. Here it is:
 It turns out that it is well solvable analytically. Quite gratifying! ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) The only problem was that my program took 27 minutes to converge to a unique solution... |
|
|
|
|
Posted on: Wed Nov 21, 2012 4:19 pm Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
giulio wrote: As today calcudocu.org dindn't publish a 9x9, I generated a puzzle with the same pattern clm commented on. I wanted to see whether it would also be too difficult [for me] to solve analytically. Here it is: ... It turns out that it is well solvable analytically. Quite gratifying! ![BigGrin [biggrin]](./images/smilies/msp_biggrin.gif) The only problem was that my program took 27 minutes to converge to a unique solution... Yes, it must a be problem, 27 minutes !!! … it looks too much … you should revise your program … the solution took me around 25 minutes   (same as you, in general I also like to do the big puzzles with pen and paper though in this case it's mandatory (same as you, in general I also like to do the big puzzles with pen and paper though in this case it's mandatory  ). Now, seriously, in my opinion this second puzzle is parsecs away from your first proposal, and I am very surprised at it because the pattern is the same but this second one is quite “easy”, in fact I think it’s more or less as the normal 9x9’s in calcudoku.org (and much easier than the ones on tuesdays). ). Now, seriously, in my opinion this second puzzle is parsecs away from your first proposal, and I am very surprised at it because the pattern is the same but this second one is quite “easy”, in fact I think it’s more or less as the normal 9x9’s in calcudoku.org (and much easier than the ones on tuesdays).The reason could be: In the first puzzle we only had one number initially defined (the 3 in e5, apart of the 9 of row 5 in d5, and consequently the 1 in d6, analytically deduced because the 9 can not be an operand in the cages involving row 5, that is, “336x”, “2:” and “160x”). But in this puzzle we have several numbers “virtually” placed (with very little analysis): b3 = 5, b4 = 1, c4 =5 >>> “7-” = [2,9]; since a 5 must be in f2 or g2 >>> i1 = 5, i2 = 8. The cage “2160x” has the only possible combination [5,6,8,9] then i6 = 6 and g5-h5-i5 = [5,8,9]. Also e6 = 5 (the only available position for a 5 in column “e”) and now in column “a” the 5 must go to “7+” = [2,5] since there is a 5 in every row from 1 thru 6 and a 5 is not a factor of “864x” … . Also the 1 of row 6 must go to d6 (unique since now f6 is not valid and the 1 is not an operand in “864x” or “96x”) >>> d5 = 3 >>> c8 = 3 >>> d7-d8 = [5,7]. Obviously “5+” (f4-f5) = [2,3] with f4 = 3, f5 = 2 (due to a 2 present in d4-e4 which is equal to [2,9]) (the combination [1,4] is invalid for “5+” since it would make impossible the cage “64x” that has [1,2,4,8] as the only valid combination with two lines), etc. … suddenly many numbers are defined; the rest of the combinations are reduced quickly … (btw, the other three “perpendicular” cages “3:” facilitate the solution, etc.). (For reference, row 7 of my solution: 639714582) |
|
|
|
|
Posted on: Wed Nov 21, 2012 4:25 pm Posts: 857 Joined: Fri May 13, 2011 6:51 pm |
Hi giulio, apologize for giving a row of the solution in my previous post, too early
![Confused [confused]](./images/smilies/msp_confused.gif) . . |
|
|
|
|
Posted on: Thu Nov 22, 2012 1:49 am Posts: 54 Joined: Thu Nov 03, 2011 8:52 am |
Hi clm,
Your row 7 is correct and there is no need to apologise. The people who visit this forum don't seem to be so interested and, in any case, except for people with eidetic memory, it is is easy not to look at the nine numbers long enough to memorise them! Yes, this second puzzle is significantly easier than the previous one. This is about the level of difficulty I like, although it could be a bit more difficult. It provides a mental exercise without reaching frustration levels. The program sometimes takes so long to converge because it spends a lot of time in solving the puzzles to check for unicity of the solution, both the tentive puzzles (then abandoned) and the final one. It uses a brute-force approach, and when it has to go through many combinations for each cage, it needs to backtrack a lot. I didn't care to optimise it because I never intended to use it for instant generation. There is some correlation between the difficulty of the puzzle and how long it takes to the program, but it isn't strict. It clearly depends on where the cages that are "key" to the solution happen to be within the puzzle. Unfortunately, Patrick prefers not to tell us how he grades puzzles. If he did, I'm sure it would open up an interesting (and hot) debate. As far as I know, there are no widely used ways of grading the difficulty of CalcuDokus. Patrick could put his stamp on that if he "open-sourced" his grading algorithm. It would probably be improved as a result, because several people would contribute to it. I would like to grade my puzzles, and compare them with grades of KenKen, KenDoku, and MathDoku. It would also be fun to compare the various programs on the basis of the distribution of difficulties of the puzzles they generate. Sooner or later, I will have to tackle the issue of grading, but I believe that theory alone wouldn't cut it. A starting point could be to define parameters that could conceivably affect the difficulty of a puzzle (as usual, I would concentrate on the 9x9s). I'm thinking of number, shape, and size of cages, distribution of operations, crossings, and distribution of number of combinations and permutations, and whatever else I could come up with. Then, I would pick, say, ten puzzles of different difficulties (as perceived by me, to get started) and have them graded from 1 to 10 by, say, 1000 people. A study of the correlations between the different parameters and the perceived difficulty should result in a semi-empirical grading formula. I expect that some parameters would turn out to be irrelevant and could be discarded. It is also possible that some significant parameters would be missing. This would result in mismatches between the grade obtained with the formula and the perceived difficulty, and could only be resolved by increasing the size of the sample and "invent" further parameters. If I decide to embark in such an enterprise, I will announce it in this forum and ask for volunteers. But don't hold your breath just yet! ![Smile [smile]](./images/smilies/msp_smile.gif) |
|
|
|
|
Posted on: Fri Nov 23, 2012 4:15 pm Posts: 84 Joined: Fri May 13, 2011 9:37 am |
Hi Gulio,
The pmn-specs of the first puzzle are: 9 4,-,a1b1 480,x,c1d1d2d3 432,x,e1f1e2e3 28,x,g1h1h2 2,-,i1i2 16,+,a2b2a3 14,+,c2c3 17,+,f2g2f3 14,+,b3b4c4 1,-,g3h3 210,x,i3g4h4i4 336,x,a4a5b5c5 14,+,d4e4 2,:,f4f5 9,x,d5d6 3,e5 160,x,g5h5i5i6 1080,x,a6b6c6a7 2,-,e6f6 14,+,g6h6h7 4,-,b7c7 14,+,d7c8d8 16,+,e7e8d9e9 1344,x,f7f8f9g9 2,:,g7g8 216,x,i7h8i8 2,:,a8a9 10,+,b8b9c9 45,x,h9i9 and the second one: 9 5,-,a1b1 336,x,c1d1d2d3 576,x,e1f1e2e3 18,x,g1h1h2 40,x,i1i2 17,+,a2b2a3 3,:,c2c3 315,x,f2g2f3 25,x,b3b4c4 3,:,g3h3 21,+,i3g4h4i4 20,+,a4a5b5c5 7,-,d4e4 5,+,f4f5 3,:,d5d6 6,e5 2160,x,g5h5i5i6 864,x,a6b6c6a7 2,-,e6f6 96,x,g6h6h7 3,:,b7c7 105,x,d7c8d8 504,x,e7e8d9e9 64,x,f7f8f9g9 11,+,g7g8 18,x,i7h8i8 7,+,a8a9 96,x,b8b9c9 4,-,h9i9 My program solves the first one in 737 seconds, with 540 reboots. And then some 2000 reboots more to prove its uniqueness. So this one is very, very difficult. My pc is an i5 on 2.8 GHz, and the system uses some basic logic, naked pairs included. But of coarse not all the logic CLM is capable of!! The second puzzle is solved in 3.3 seconds with only logic. So this one is easy. Dag, NicoW |
|
|
|
|
|
Page 1 of 2 |
[ 17 posts ] | Go to page 1, 2 Next |
|
All times are UTC + 1 hour [ DST ] |
| You cannot post new topics in this forum You cannot reply to topics in this forum You cannot edit your posts in this forum You cannot delete your posts in this forum |