The 10 Hardest Logic/Number Puzzles |
| Tweet | ||
The goal of this mini-project is to find and describe the 10 hardest logic and/or number puzzles out there. The current list is by no means definitive, your comments and suggestions are more than welcome at .
The puzzles, in no particular order:
1. The World's Hardest Sudoku
Sudoku is easily the most played and most analyzed puzzle in the world, so coming
up with the hardest one is no mean feat.
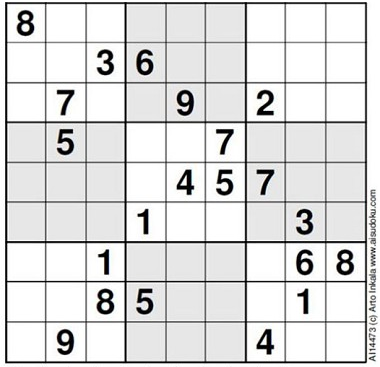 In 2012, Finnish mathematician Arto Inkala claimed to have created the "World's Hardest Sudoku",
which
the Telegraph rated "11 out of 5 stars":-).
Arto's web site has more information on how the puzzles are rated.
In 2012, Finnish mathematician Arto Inkala claimed to have created the "World's Hardest Sudoku",
which
the Telegraph rated "11 out of 5 stars":-).
Arto's web site has more information on how the puzzles are rated.
At Sudokuwiki.org it is claimed that Arto's puzzle is the 3rd known hardest (although apparently the hardest puzzle listed there is in fact relatively easy). Their discussion of rating Sudoku puzzles.
↑ Back to top
2. The Hardest Logic Puzzle Ever
American philosopher and logician George Boolos described this puzzle (and called it "The Hardest Logic Puzzle Ever" :-), devised by Raymond Smullyan and published in the Harvard Review of Philosophy in 1996:
Three gods A, B, and C are called, in no particular order, True, False, and Random. True always speaks truly, False always speaks falsely, but whether Random speaks truly or falsely is a completely random matter. Your task is to determine the identities of A, B, and C by asking three yes-no questions; each question must be put to exactly one god. The gods understand English, but will answer all questions in their own language, in which the words for yes and no are da and ja, in some order. You do not know which word means which.The original article can be downloaded here. You can read about making this puzzle even harder on the Physics arXiv Blog. ↑ Back to top
3. One of the World's Hardest Killer Sudokus
A Killer Sudoku is very similar to a Sudoku, except that the clues are given as groups of cells + the sum of the numbers in those cells. Check out the Wikipedia page on Killer Sudoku for more information.

From a large number of highest rated puzzles at calcudoku.org/killersudoku, we measured what percentage of puzzlers solved them on the day
they were published. Easily the hardest was the Killer Sudoku published on the 9th of November 2012 shown here
(click on the puzzle to try and solve it yourself!).
↑ Back to top
4. The Hardest Bongard Problem
This type of puzzle first appeared in a book by Russian scientist M. Bongard in 1967.
They became more widely known after Douglas Hofstadter mentioned them in his book
"Gödel, Escher, Bach".
 Easily the most information on Bongard problems
can be found on Harry Foundalis' site.
Easily the most information on Bongard problems
can be found on Harry Foundalis' site.
To solve the puzzle, you have to find a rule that the 6 patterns on the left hand side conform to. The 6 patterns on the right do not conform to this rule.
For example, the first problem on this page has as a solution: all patterns on the left are triangles.
↑ Back to top
5. The Hardest Calcudoku Puzzle
A Calcudoku is similar to a Killer Sudoku, except that (1) any operation can be used
to compute the result of a "cage" (not only addition), (2) the puzzle can be any square size,
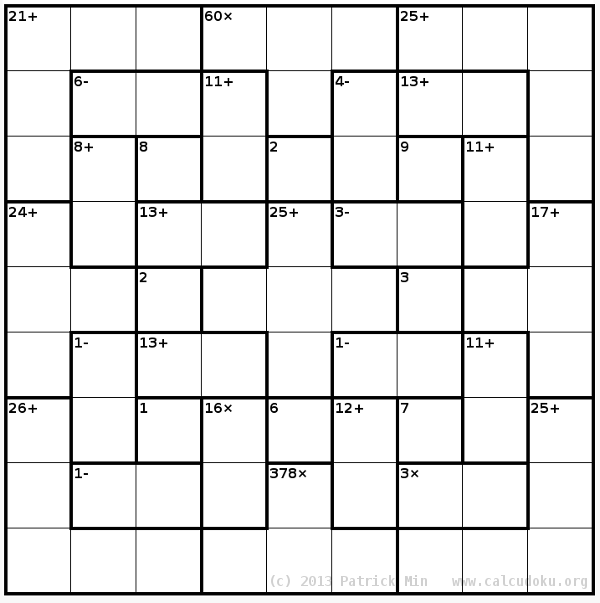 and (3) the Sudoku rule of requiring the numbers 1..9 in each 3×3 set of cells does not apply.
It was invented by Japanese math teacher Tetsuya Miyamoto, who called it "Kashikoku naru" ("smartness").
and (3) the Sudoku rule of requiring the numbers 1..9 in each 3×3 set of cells does not apply.
It was invented by Japanese math teacher Tetsuya Miyamoto, who called it "Kashikoku naru" ("smartness").
Identified in the same way as the Killer Sudoku puzzle shown above, the hardest Calcudoku was a 9×9 puzzle published on the 2nd of April 2013, which only 9.6% of the regular puzzlers at calcudoku.org managed to solve. Click on the puzzle to try and solve it yourself :-).
If you're not up for solving it yourself, check out this step-by-step solving analysis by "clm".
A Calcudoku variation using the modulo operator is a good candidate as well. It appeared in the Calcudoku, 101 Advanced Puzzles book, and clearly was the least-solved puzzle, with one math professor writing that it took him 5 hours to solve, spread over multiple days... If you'd like to try it yourself, you can find it here.
↑ Back to top
6. The Hardest "Ponder this" Puzzle
IBM Research has been publishing very challenging monthly puzzles since May 1998 on their "Ponder this" page. Judging from the number of solvers for each, the hardest number puzzle is the one from April 2009:
Design a storage system that encodes 24 information bits on 8 disks of 4 bits each, such that:Go to the April 2009 Challenge page if you need some clues :-). ↑ Back to top
- Combining the 8*4 bits into a 32 bits number (taking a nibble from each disk), a function f from 24 bits to 32 can be computed using only 5 operations, each of which is out of the set {+, -, *, /, %, &, |, ~} (addition; subtraction, multiplication; integer division, modulo; bitwise-and; bitwise-or; and bitwise-not) on variable length integers. In other words, if every operation takes a nanosecond, the function can be computed in 5 nanoseconds.
- One can recover the original 24 bits even after any 2 of the 8 disks crash (making them unreadable and hence loosing 2 nibbles)
7. The Hardest Kakuro Puzzle
The Kakuro puzzle combines elements of Sudoku, logic, crosswords, and basic math into one.
From the Wikipedia page on Kakuro:
 "The objective of the puzzle is to insert a digit from 1 to 9
inclusive into each white cell such that the sum of the numbers in
each entry matches the clue associated with it and that no digit is
duplicated in any entry".
"The objective of the puzzle is to insert a digit from 1 to 9
inclusive into each white cell such that the sum of the numbers in
each entry matches the clue associated with it and that no digit is
duplicated in any entry".
Those in the know tell me that the "Absolutely Nasty Kakuro" series has the hardest Kakuro puzzles. Conceptis puzzles produced an even nastier specimen especially for this article (!)
↑ Back to top
8. Martin Gardner's Hardest Puzzle
In Martin Gardner's book The Colossal Book of Short Puzzles and Problems, puzzles in many categories are listed in order of difficulty. This is the hardest puzzle from the "Numbers" chapter:
A number's persistence is the number of steps required to reduce it to a single digit by multiplying all its digits to obtain a second number, then multiplying all the digits of that number to obtain a third number, and so on until a one-digit number is obtained. For example, 77 has a persistence of four because it requires four steps to reduce it to one digit: 77-49-36-18-8. The smallest number of persistence one is 10, the smallest of persistence two is 25, the smallest of persistence three is 39, and the smaller of persistence four is 77. What is the smallest number of persistence five?Can the answer be derived? Also, since he wrote so many books, articles, etc.: is there a harder logic/number puzzle by Martin Gardner? ↑ Back to top
9. The Most Difficult Go Problem Ever
From the Wikipedia page on Go: "Go is a board game for two players that originated in China more than 2,500 years ago. The game is noted for being rich in strategy despite its relatively simple rules."
This problem is considered to be the hardest ever, and is said
to have taken 1000 hours to solve by a group of high level students.
 Solutions and many references can be found on
this page.
Solutions and many references can be found on
this page.
↑ Back to top
10. The Hardest Fill-a-Pix Puzzle
Fill-a-Pix is a Minesweeper-like puzzle based on a grid with a pixilated picture hidden inside. Using logic alone, the solver determines which squares are painted and which should remain empty until the hidden picture is completely exposed. Advanced logic Fill-a-Pix such as the one above contain situations where two clues simultaneously affect each other as well as the squares around them making these puzzles extremely hard to solve.
Fill-a-Pix was invented by Trevor Truran, a former high-school math teacher and the editor of Hanjie and several other famed British magazines published by Puzzler Media.
 For Fill-a-Pix solving rules, advanced solving techniques and more
about the history of this puzzle check the
Get started section on
conceptispuzzles.com. This ultra-hard puzzle was generated by
Conceptis especially for this article (click on the image for a PDF version).
For Fill-a-Pix solving rules, advanced solving techniques and more
about the history of this puzzle check the
Get started section on
conceptispuzzles.com. This ultra-hard puzzle was generated by
Conceptis especially for this article (click on the image for a PDF version).
↑ Back to top
Your comments and suggestions are very welcome at .
If these puzzles give you headaches, instead check out the World's Easiest Logic/Number Puzzles.
And now you may want to solve Sudoku, Killer Sudoku, and Calcudoku puzzles online yourself :-)
© Patrick Min, 2013
